题目内容
椭圆T的中心为坐标原点O,右焦点为F(2,0),且椭圆T过点E(2,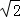 ).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.
).△ABC的三个顶点都在椭圆T上,设三条边的中点分别为M,N,P.
(1)求椭圆T的离心率;
(2)设△ABC的三条边所在直线的斜率分别为k1,k2,k3,且ki≠0,i=1,2,3.若直线OM,ON,OP的斜率之和为0,求证: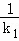 +
+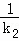 +
+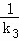 为定值.
为定值.
解答: (1)解:设椭圆T的方程为 ,
,
由题意知:左焦点为F′(﹣2,0),∴2a=|EF|+|EF′|= ,
,
解得: .
.
故椭圆T的离心率为 ;
;
(2)证明:由(1)知椭圆T的方程为 .
.
设A(x1,y1),B(x2,y2),C(x3,y3),
M(s1,t1),N(s2,t2),P(s3,t3),
由: ,
, ,两式相减,得到
,两式相减,得到
(x1﹣x2)(x1+x2)+2(y1﹣y2)(y1+y2)=0.
∴ ,即
,即 ,
,
同理 ,
, .
.
∴ ,
,
又∵直线OM、ON、OP的斜率之和为0,
∴ +
+ +
+ =0为定值.
=0为定值.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 .
.
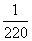 B.
B.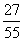
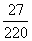 D.
D.
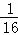 a)的定义域为R,命题q:q:不等式
a)的定义域为R,命题q:q:不等式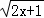 <1+ax对一切正实数x均成立.如果,命题“p∨q”为真命题,命题“p∧q”为假命题,则实数a的取值范围为( )
<1+ax对一切正实数x均成立.如果,命题“p∨q”为真命题,命题“p∧q”为假命题,则实数a的取值范围为( ) -x(x≥0)的最大值为________.
-x(x≥0)的最大值为________.