题目内容
中国共产党第十八届中央委员会第二次全体会议于2013年2月26日至28日在北京顺利举行,两名大学生志愿者甲与乙被安排在26日下午参加接待工作,工作时间均在13时至18时之间,已知甲连续工作2小时,乙连续工作3小时,则17时甲、乙都在工作的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:设出甲乙开始的时刻,求出满足条件的不等式组,作出对应的平面区域,利用几何概型的概率公式即可得到结论.
解答:
解:设甲开始的时刻为x,乙开始学习的时刻为y,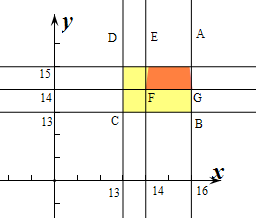
则试验的全部结果为M={(x,y)|
},区域面积S=3×2=6,
则17时甲、乙都在工作结果为N={(x,y)|
},区域面积S=2×1=2,
则作出对应的平面区域如图:
区域M面积S=3×2=6,区域N面积S=2×1=2,
则17时甲、乙都在工作的概率是
=
,
故选:C

则试验的全部结果为M={(x,y)|
|
则17时甲、乙都在工作结果为N={(x,y)|
|
则作出对应的平面区域如图:
区域M面积S=3×2=6,区域N面积S=2×1=2,
则17时甲、乙都在工作的概率是
| 2 |
| 6 |
| 1 |
| 3 |
故选:C
点评:本题主要考查几何概型的概率的计算,求出对应的区域面积是解决本题的关键.

练习册系列答案
相关题目
在正四棱锥P-ABCD中,PA=2,直线PA与平面ABCD所成角为60°,E为PC的中点,则异面直线PA与BE所成角为( )
| A、90° | B、60° |
| C、45° | D、30° |
已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ<2π)图象上的一个最高点是(2,
),由这个最高点到相邻的最低点图象与x轴的交点为(6,0),则f(x)=( )
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列函数在[0,+∞)内为增函数的是( )
| A、y=x2-x | ||
B、y=-
| ||
| C、y=lnx | ||
| D、y=ex |
已知函数f(x)=-|x|,则f(x)是( )
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇函数非偶函数 |