题目内容
已知曲线C1: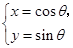 (
( 为参数),曲线C2:
为参数),曲线C2: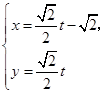 (t为参数).
(t为参数).
(1)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线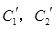 .写出
.写出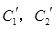 的参数方程.
的参数方程.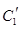 与
与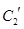 公共点的个数和C
公共点的个数和C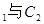 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.
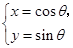 (
( 为参数),曲线C2:
为参数),曲线C2: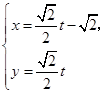 (t为参数).
(t为参数).(1)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线
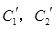 .写出
.写出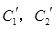 的参数方程.
的参数方程.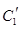 与
与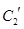 公共点的个数和C
公共点的个数和C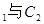 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.(1)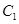 的普通方程为
的普通方程为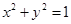 ,
,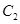 的普通方程为
的普通方程为 ,所以
,所以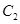 与
与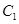 只有一个公共点;(2)压缩后的直线
只有一个公共点;(2)压缩后的直线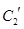 与椭圆
与椭圆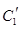 仍然只有一个公共点,和
仍然只有一个公共点,和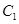 与
与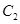 公共点个数相同.
公共点个数相同.
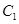 的普通方程为
的普通方程为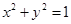 ,
,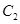 的普通方程为
的普通方程为 ,所以
,所以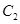 与
与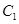 只有一个公共点;(2)压缩后的直线
只有一个公共点;(2)压缩后的直线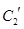 与椭圆
与椭圆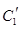 仍然只有一个公共点,和
仍然只有一个公共点,和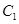 与
与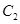 公共点个数相同.
公共点个数相同.试题分析:本题主要考查参数方程与普通方程的互化、直线与圆的位置关系、直线与椭圆的位置关系等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,利用参数方程中参数将参数方程转化成普通方程,判断图形形状,再利用圆心到直线的距离与半径的关系判断直线与圆的位置关系;第二问,先将原
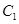 和
和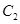 的纵坐标压缩为原来的一半,得到曲线
的纵坐标压缩为原来的一半,得到曲线 和
和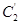 的参数方程,再转化成普通方程得到直线和椭圆,2个方程联立,消参,利用判别式判断有几个交点.
的参数方程,再转化成普通方程得到直线和椭圆,2个方程联立,消参,利用判别式判断有几个交点.试题解析:(1)
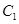 是圆,
是圆, 是直线.
是直线. 的普通方程为
的普通方程为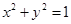 ,圆心
,圆心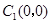 ,半径
,半径 .
.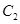 的普通方程为
的普通方程为 . 2分
. 2分因为圆心
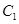 到直线
到直线 的距离为
的距离为 ,
,所以
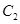 与
与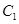 只有一个公共点. 4分
只有一个公共点. 4分(2)压缩后的参数方程分别为
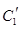 :
: (
( 为参数);
为参数); 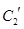 :
: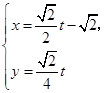 (t为参数).
(t为参数).化为普通方程为:
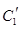 :
: ,
,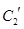 :
: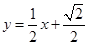 , 6分
, 6分联立消元得
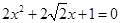 ,
,其判别式
 , 7分
, 7分所以压缩后的直线
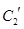 与椭圆
与椭圆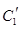 仍然只有一个公共点,和
仍然只有一个公共点,和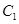 与
与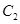 公共点个数相同.
公共点个数相同.
练习册系列答案
相关题目
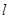 的参数方程为
的参数方程为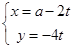 ,(
,(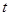 为参数),圆
为参数),圆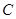 的参数方程为
的参数方程为 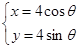 ,(
,(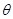 为参数).
为参数).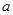 的取值范围.
的取值范围.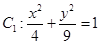 ,直线
,直线 :
: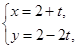 (
(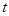 为参数).
为参数).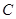 的参数方程,直线
的参数方程,直线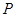 作与
作与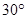 的直线,交
的直线,交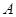 ,
,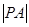 的最大值与最小值.
的最大值与最小值.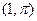 ,则过点P且垂直极轴的直线极坐标方程是 .
,则过点P且垂直极轴的直线极坐标方程是 .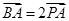 ,点P的轨迹为曲线C.
,点P的轨迹为曲线C.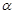 为参数,求曲线C的参数方程;
为参数,求曲线C的参数方程;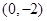 距离的最大值.
距离的最大值.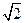 ,
,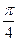 ),直线l的极坐标方程为ρcos(
),直线l的极坐标方程为ρcos(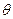
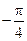 )=a,且点A在直线l上.
)=a,且点A在直线l上.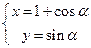 (
(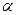 为参数),试判断直线l与圆C的位置关系.
为参数),试判断直线l与圆C的位置关系.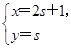 (s为参数)和直线l2:
(s为参数)和直线l2: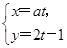 (t为参数)平行,则常数a的值为________.
(t为参数)平行,则常数a的值为________.