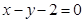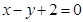题目内容
在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系.已知点A的极坐标为(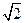 ,
,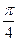 ),直线l的极坐标方程为ρcos(
),直线l的极坐标方程为ρcos(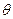
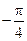 )=a,且点A在直线l上.
)=a,且点A在直线l上.
(1)求a的值及直线l的直角坐标方程;
(2)圆C的参数方程为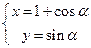 (
(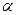 为参数),试判断直线l与圆C的位置关系.
为参数),试判断直线l与圆C的位置关系.
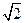 ,
,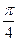 ),直线l的极坐标方程为ρcos(
),直线l的极坐标方程为ρcos(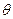
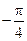 )=a,且点A在直线l上.
)=a,且点A在直线l上.(1)求a的值及直线l的直角坐标方程;
(2)圆C的参数方程为
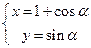 (
(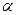 为参数),试判断直线l与圆C的位置关系.
为参数),试判断直线l与圆C的位置关系.(1)x+y-2=0 (2)相交
(1)由点A(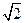 ,
,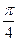 )在直线ρcos(
)在直线ρcos(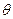 -
-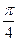 )=a上,可得a=
)=a上,可得a=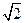 ,所以直线l的方程可化为
,所以直线l的方程可化为 ,从而直线l的直角坐标方程为
,从而直线l的直角坐标方程为 .
.
(2)由已知得圆C的直角坐标方程为(x-1)2+y2=1,所以圆C的圆心为(1,0),半径r=1,因为圆心C到直线l的距离d= <1,所以直线l与圆C相交.
<1,所以直线l与圆C相交.
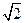 ,
,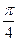 )在直线ρcos(
)在直线ρcos(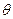 -
-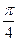 )=a上,可得a=
)=a上,可得a=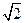 ,所以直线l的方程可化为
,所以直线l的方程可化为 ,从而直线l的直角坐标方程为
,从而直线l的直角坐标方程为 .
.(2)由已知得圆C的直角坐标方程为(x-1)2+y2=1,所以圆C的圆心为(1,0),半径r=1,因为圆心C到直线l的距离d=
 <1,所以直线l与圆C相交.
<1,所以直线l与圆C相交.
练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
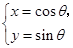 (
( 为参数),曲线C2:
为参数),曲线C2: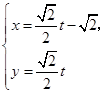 (t为参数).
(t为参数).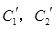 .写出
.写出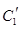 与
与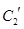 公共点的个数和C
公共点的个数和C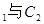 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.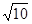 ,0)作直线l,交曲线
,0)作直线l,交曲线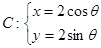 (θ为参数)于A,B两点,若|MA|,|AB|,|MB|成等比数列,求直线l的方程.
(θ为参数)于A,B两点,若|MA|,|AB|,|MB|成等比数列,求直线l的方程.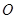 的半径为
的半径为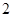 ,圆
,圆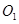 ,
,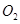 ,
,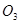 为球
为球 ,
,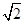 ,
,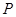 ,则
,则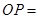
 (t为参数)与直线
(t为参数)与直线 垂直,则常数
垂直,则常数 = .
= .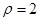 上的点到直线
上的点到直线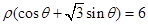 的距离的最小值为________.
的距离的最小值为________. 的圆心到直线
的圆心到直线 的距离是 .
的距离是 .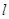 的参数方程为
的参数方程为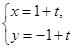 (
(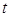 为参数),则直线
为参数),则直线