题目内容
已知椭圆C的中心点在原点，焦点M、N在x轴上，且焦距为2
，长轴长为4
（1）求椭圆C的方程；
（2）在椭圆C上是否存在一点Q，使得∠MQN为钝角？若存在，求出Q点横坐标的取值范围；若不存在，请说明理由．
| 3 |
（1）求椭圆C的方程；
（2）在椭圆C上是否存在一点Q，使得∠MQN为钝角？若存在，求出Q点横坐标的取值范围；若不存在，请说明理由．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（Ⅰ）设椭圆方程为
+
=1，由焦距为2
，实轴长为4，能求出椭圆C的方程．
（Ⅱ）假设存在，设Q（x，y），由∠MQN为钝角，知
•
＜0，从而得到
•
=x2+y2-3＜0，与
+y2=1联立，能求出Q点横坐标的取值范围．
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
（Ⅱ）假设存在，设Q（x，y），由∠MQN为钝角，知
| QM |
| QN |
| QM |
| QN |
| x2 |
| 4 |
解答：
解：（Ⅰ）设椭圆方程为
+
=1，
∵且焦距为2
，长轴长为4，
∴a=2，c=
，b2=4-3=1，
∴椭圆C的方程为
+y2=1．
（Ⅱ）假设存在，设Q（x，y），
∵∠MQN为钝角，∴
•
＜0，
∵焦点M（-
，0）、N（
，0），
∴
=(-
-x，-y)，
=(
-x．-y)，
∴
•
=x2+y2-3＜0，
又∵Q点在椭圆上，∴
+y2=1，
联立两式，得：x2+1-
-3＜0，
化简，得x2＜
．
解得出Q点横坐标的取值范围是（-
，
）．
∴椭圆C上存在一点Q，使得∠MQN为钝角，Q点横坐标的取值范围是（-
，
）．
| x2 |
| a2 |
| y2 |
| b2 |
∵且焦距为2
| 3 |
∴a=2，c=
| 3 |
∴椭圆C的方程为
| x2 |
| 4 |
（Ⅱ）假设存在，设Q（x，y），
∵∠MQN为钝角，∴
| QM |
| QN |
∵焦点M（-
| 3 |
| 3 |
∴
| QM |
| 3 |
| QN |
| 3 |
∴
| QM |
| QN |
又∵Q点在椭圆上，∴
| x2 |
| 4 |
联立两式，得：x2+1-
| x2 |
| 4 |
化简，得x2＜
| 8 |
| 3 |
解得出Q点横坐标的取值范围是（-
2
| ||
| 3 |
2
| ||
| 3 |
∴椭圆C上存在一点Q，使得∠MQN为钝角，Q点横坐标的取值范围是（-
2
| ||
| 3 |
2
| ||
| 3 |
点评：本题考查椭圆方程的求法，考查满足钝角的点的坐标是否存在的判断与求法，解题时要认真审题，注意向量数量积的灵活运用．
练习册系列答案
名校课堂系列答案
相关题目
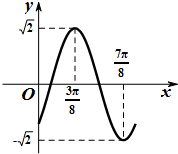已知函数f（x）=asin（ωx+θ）的部分图象如下图，其中ω＞0，|θ|＜
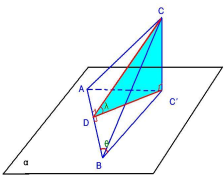如图，已知△ABC在平面α内的射影为△ABC′，若∠ABC′=θ，BC′=a，且平面ABC与平面α所成的角为λ，求点C到平面α的距离．