题目内容
已知曲线C：x2+y2=4（x≥0，y≥0）与函数f（x）=log2x，g（x）=2x的图象分别交于A（x1，y1），B（x2，y2），则x12+x22= ．
考点：圆方程的综合应用
专题：直线与圆
分析：通过函数与反函数的对称关系，判断AB的坐标关系，然后求解即可．
解答：
解：由于函数f（x）=log2x，g（x）=2x互为反函数，
∴A（x1，y1），B（x2，y2）关于直线y=x对称，
∴x2=y1．∵A（x1，y1）在曲线C上，
∴x12+y12=x12+x22=4，
故答案为：4．
∴A（x1，y1），B（x2，y2）关于直线y=x对称，
∴x2=y1．∵A（x1，y1）在曲线C上，
∴x12+y12=x12+x22=4，
故答案为：4．
点评：本题考查圆的方程的应用，反函数与原函数的对称关系，点的坐标与切线方程的应用，考查计算能力以及转化思想的应用．
练习册系列答案
相关题目
下列命题错误的是（ ）
| A、命题“若x2+y2≠0，则x=y=0”的逆否命题为“若x，y中至少有一个不为0，则x2+y2≠0” |
| B、若命题p：?x0∈R，使得x02-x0+1≤0；则￢p：?x∈R，均有x2-x+1＞0 |
| C、若p∧q为假命题，则p∨￢q为真命题 |
| D、“x＞|y|”是“x2＞y2”的充分不必要条件 |
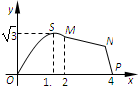如图，某市拟在长为4km的道路OP的一侧修建一条运动赛道，赛道的前一部分为曲线段OSM，该曲线段为函数y=Asinωx（A＞0，ω＞0），X∈[0，2]的图象，且图象的最高点为S（若a＜b＜0，则下列不等式一定成立的是（ ）
A、
| ||||
| B、a2＜ab | ||||
C、
| ||||
| D、an＞bn |