题目内容
【题目】已知函数![]() (其中
(其中![]() 是实数).
是实数).
(1)求![]() 的单调区间;
的单调区间;
(2)若设![]() ,且
,且![]() 有两个极值点
有两个极值点![]() ,
,![]() (
(![]() ),求
),求![]() 取值范围.(其中
取值范围.(其中![]() 为自然对数的底数).
为自然对数的底数).
【答案】(1)当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间,当
,无单调递减区间,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)求出![]() 的定义域为
的定义域为![]() ,
,![]() ,由此利用导数性质和分类讨论思想能求出
,由此利用导数性质和分类讨论思想能求出![]() 的单调区间;(2)推导出
的单调区间;(2)推导出![]() ,令
,令![]() ,则
,则![]() 恒成立,由此能求出
恒成立,由此能求出![]() 的取值范围.
的取值范围.
试题解析:(1)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
令![]() ,
,![]() ,对称轴
,对称轴![]() ,
,![]() ,
,
(1)当![]() ,即
,即![]() 时,
时,![]()
于是,函数![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间.
,无单调递减区间.
(2)当![]() ,即
,即![]() 或
或![]() 时,①若
时,①若![]() ,则
,则![]() 恒成立
恒成立
于是,![]() 的单调递增区间为
的单调递增区间为![]() ,无减区间.②若
,无减区间.②若![]()
令![]() ,得
,得![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
于是,![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() .综上所述:
.综上所述:
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间.
,无单调递减区间.
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)由(1)知,若![]() 有两个极值点,则
有两个极值点,则![]() ,且
,且![]() ,
,![]() ,
,
![]()
又![]() ,
,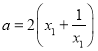 ,
,![]() ,
,![]() ,又
,又![]() ,解得,
,解得,![]() 于是,
于是,![]()
![]()
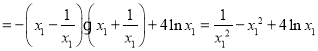
令![]() (
(![]() ),则
),则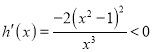 恒成立,
恒成立,![]() 在
在![]() 单调递减,
单调递减,![]() ,即
,即![]() ,故
,故![]() 的取值范围为
的取值范围为![]()

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
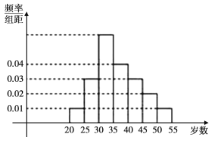
【题目】高一年级某个班分成7个小组,利用假期参加社会公益服务活动![]() 每个小组必须全员参加
每个小组必须全员参加![]() ,参加活动的次数记录如下:
,参加活动的次数记录如下:
组别 |
|
|
|
|
|
|
|
参加活动次数 | 3 | 2 | 4 | 3 | 3 | 4 | 2 |
![]() Ⅰ
Ⅰ![]() 求该班的7个小组参加社会公益服务活动数的中位数及与平均数v;
求该班的7个小组参加社会公益服务活动数的中位数及与平均数v;
![]() Ⅱ
Ⅱ![]() 从这7个小组中随机选出2个小组在全校进行活动汇报,求“选出的2个小组参加社会公益服务活动次数相等”的概率.
从这7个小组中随机选出2个小组在全校进行活动汇报,求“选出的2个小组参加社会公益服务活动次数相等”的概率.
![]() Ⅲ
Ⅲ![]() 至
至![]() 小组每组有4名同学,
小组每组有4名同学,![]() 小组有5名同学,记“该班学参加社会公益服务活动的平均次数”为
小组有5名同学,记“该班学参加社会公益服务活动的平均次数”为![]() ,写出
,写出![]() 与v的大小关系
与v的大小关系![]() 结论不要求证明
结论不要求证明![]() .
.