题目内容
5.已知复数${z_1}=\frac{3}{a+2}+({a^2}-3)i$,z2=2+(3a+1)i(a∈R,i是虚数单位).(1)若z1∈R,求a的值;
(2)若复数z1-z2在复平面上对应点落在第一象限,求实数a的取值范围.
分析 (1)利用复数的基本概念,虚部为0,求解即可.
(2)化简复数,求出对应点的坐标,列出不等式组求解即可.
解答 解:(1)复数${z_1}=\frac{3}{a+2}+({a^2}-3)i$,z1∈R,可得a2-3=0,
解得:$a=±\sqrt{3}$;
(2)由条件复数${z_1}=\frac{3}{a+2}+({a^2}-3)i$,z2=2+(3a+1)i
得,${z_1}-{z_2}=(\frac{3}{a+2}-2)+({a^2}-3a-4)i$
因为z1-z2在复平面上对应点落在第一象限,
故有$\left\{\begin{array}{l}\frac{3}{a+2}-2>0\\{a^2}-3a-4>0\end{array}\right.$,
∴$\left\{\begin{array}{l}-2<a<-\frac{1}{2}\\ a>4或a<-1\end{array}\right.$,
解得-2<a<-1.
点评 本题考查复数的基本概念,复数的几何意义,考查计算能力.

练习册系列答案
相关题目
11.已知集合A={y|y=$\sqrt{{x}^{2}-1}$},B={x|x2-1<0},则A∩B=( )
| A. | ∅ | B. | {x|0≤x<1} | C. | {x|x≥0} | D. | {x|0<x<1} |
17.执行如图的程序框图,若输入的a,b,k分别为1,2,4,则输出的M=( )


| A. | $\frac{8}{3}$ | B. | $\frac{15}{8}$ | C. | $\frac{16}{5}$ | D. | $\frac{20}{3}$ |
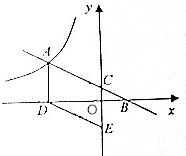 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E,已知四边形ADEC的面积为6.
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A,与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E,已知四边形ADEC的面积为6.