题目内容
7.证明:$\sum_{i=1}^{n}$r${C}_{n}^{r}$=n2n-1.分析 根据组合数的公式,结合二项式定理,进行变形、应用即可.
解答 证明:∵$\underset{\stackrel{n}{∑}}{r=1}$r${C}_{n}^{r}$=$\underset{\stackrel{n}{∑}}{r=1}$n${C}_{n-1}^{r-1}$
=n$\underset{\stackrel{n}{∑}}{r=1}$${C}_{n-1}^{r-1}$
=n$\underset{\stackrel{n-1}{∑}}{s=0}$${C}_{n-1}^{s}$
=n(${C}_{n-1}^{0}$+${C}_{n-1}^{1}$+…+${C}_{n-1}^{n-1}$)=n2n-1.
点评 本题考查了组合数公式的应用问题,也考查了二项式定理的应用问题,是基础题目.

练习册系列答案
相关题目
15.设函数f(x)对x≠0的实数满足f(x)-2f($\frac{1}{x}$)=3x+2,那么${∫}_{1}^{2}$f(x)dx=( )
| A. | -($\frac{7}{2}$+2ln2) | B. | $\frac{7}{2}$+2ln2 | C. | -($\frac{7}{2}$+ln2) | D. | -(4+2ln2) |
12.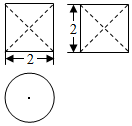 如图为一个圆柱中挖去两个完全相同的圆锥而形成的几何体的三视图,则该几何体的体积为( )
如图为一个圆柱中挖去两个完全相同的圆锥而形成的几何体的三视图,则该几何体的体积为( )
 如图为一个圆柱中挖去两个完全相同的圆锥而形成的几何体的三视图,则该几何体的体积为( )
如图为一个圆柱中挖去两个完全相同的圆锥而形成的几何体的三视图,则该几何体的体积为( )| A. | $\frac{1}{3}$π | B. | $\frac{2}{3}$π | C. | $\frac{4}{3}$π | D. | $\frac{5}{3}$π |