题目内容
17.tan$\frac{π}{24}$+tan$\frac{π}{24}$tan$\frac{5π}{24}$+tan$\frac{5π}{24}$=1.分析 由条件利用两角和的正切公式,求得要求式子的值.
解答 解:∵tan($\frac{π}{24}$+$\frac{5π}{24}$)=tan$\frac{π}{4}$=1=$\frac{tan\frac{π}{24}+tan\frac{5π}{4}}{1-tan\frac{π}{24}tan\frac{5π}{24}}$,
∴tan$\frac{π}{24}$+$\frac{5π}{24}$=1-tan$\frac{π}{24}$tan$\frac{5π}{24}$,
∴tan$\frac{π}{24}$+tan$\frac{π}{24}$tan$\frac{5π}{24}$+tan$\frac{5π}{24}$=1-tan$\frac{π}{24}$tan$\frac{5π}{24}$+tan$\frac{π}{24}$tan$\frac{5π}{24}$=1,
故答案为:1.
点评 本题主要考查两角和的正切公式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知$\overrightarrow{a}$、$\overrightarrow{b}$是平面内两个互相垂直的单位向量,若向量$\overrightarrow{c}$满足($\overrightarrow{c}$-$\overrightarrow{a}$)•($\overrightarrow{c}$-$\overrightarrow{b}$)=0,则|$\overrightarrow{c}$|的最大值是( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
12.若不等式组$\left\{\begin{array}{l}x-y+2≥0\\ y≥m\\ 0≤x≤2\end{array}\right.$表示的平面区域是一个三角形,则m的取值范围是( )
| A. | [2,4) | B. | [2,+∞) | C. | [2,4] | D. | (2,4] |
9.已知等比数列{an}中,各项都是正数,前n项和为Sn,且${a_2},\frac{1}{2}{a_3},{S_2}$成等差数列,则公比q等于( )
| A. | $1+\sqrt{2}$ | B. | $1-\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $3-2\sqrt{2}$ |
7.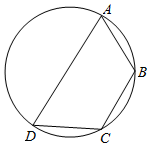 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )| A. | $\sqrt{3}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\sqrt{3}$+1 | D. | $\frac{\sqrt{3}}{2}$+$\frac{1}{2}$ |