题目内容
已知椭圆
+
=1(a>b>0)的右焦点为F,A为短轴的一个端点,且|OA|=|OF|,△AOF的面积为1(其中O为坐标原点).
(Ⅰ)求椭圆的方程;
(Ⅱ)若C、D分别是椭圆长轴的左、右端点,动点M满足MD⊥CD,连结CM,交椭圆于点P,证明:
•
为定值;
(Ⅲ)在(Ⅱ)的条件下,试问x轴上是否存在异于点C的定点Q,使得以MP为直径的圆恒过直线DP、MQ的交点,若存在,求出点Q的坐标;若不存在,说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)求椭圆的方程;
(Ⅱ)若C、D分别是椭圆长轴的左、右端点,动点M满足MD⊥CD,连结CM,交椭圆于点P,证明:
| OM |
| OP |
(Ⅲ)在(Ⅱ)的条件下,试问x轴上是否存在异于点C的定点Q,使得以MP为直径的圆恒过直线DP、MQ的交点,若存在,求出点Q的坐标;若不存在,说明理由.
考点:直线与圆锥曲线的综合问题
专题:向量与圆锥曲线
分析:(Ⅰ)由题意可知b=c,再由△AOF的面积为1求得b,c的值结合a2=b2+c2求得a2,则椭圆方程可求;
(Ⅱ)由(Ⅰ)可求C,D的坐标,设出CM所在直线方程,由MD⊥CD得到M的坐标(用CM的斜率和常数表示),联立CM的方程和椭圆方程后借助于根与系数关系求得P的坐标,
代入数量积公式可证
•
为定值;
(Ⅲ)假设存在,设出Q点坐标,由
•
=0列式求得Q点的坐标.
(Ⅱ)由(Ⅰ)可求C,D的坐标,设出CM所在直线方程,由MD⊥CD得到M的坐标(用CM的斜率和常数表示),联立CM的方程和椭圆方程后借助于根与系数关系求得P的坐标,
代入数量积公式可证
| OM |
| OP |
(Ⅲ)假设存在,设出Q点坐标,由
| QM |
| DP |
解答:
(Ⅰ)解:由已知:
,
∴b=c=
,a2=b2+c2=4,
∴椭圆方程为
+
=1;
(Ⅱ)证明:由(1)知,C(-2,0),D(2,0).
由题意可设CM:y=k(x+2),P(x1,y1).
∵MD⊥CD,
∴M(2,4k).
由
,消去y整理得:(1+2k2)x2+8k2x+8k2-4=0,
∴△=(8k2)2-4(1+2k2)(8k2-4)>0,
-2x1=
,即x1=
.
∴y1=k(x1+2)=
,
∴点P(
,
).
∴
•
=2•
+4k•
=
=4(定值).
(Ⅲ)解:设Q(x0,0),且x0≠2.
若以MP为直径的圆恒过DP,MQ的交点,
则MQ⊥DP,
∴
•
=0恒成立.
由(2)可知:
=(2-x0,4k),
=(
,
),
∴
•
=(2-x0)•
+4k•
=0,
即
x0=0恒成立,
∴x0=0.
∴存在Q(0,0),使得以MP为直径的圆恒过直线DP、MQ的交点.
|
∴b=c=
| 2 |
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 2 |
(Ⅱ)证明:由(1)知,C(-2,0),D(2,0).
由题意可设CM:y=k(x+2),P(x1,y1).
∵MD⊥CD,
∴M(2,4k).
由
|
∴△=(8k2)2-4(1+2k2)(8k2-4)>0,
-2x1=
| 8k2-4 |
| 1+2k2 |
| 2-4k2 |
| 1+2k2 |
∴y1=k(x1+2)=
| 4k |
| 1+2k2 |
∴点P(
| 2-4k2 |
| 1+2k2 |
| 4k |
| 1+2k2 |
∴
| OM |
| OP |
| 2-4k2 |
| 1+2k2 |
| 4k |
| 1+2k2 |
| 4(1+2k2) |
| 1+2k2 |
(Ⅲ)解:设Q(x0,0),且x0≠2.
若以MP为直径的圆恒过DP,MQ的交点,
则MQ⊥DP,
∴
| QM |
| DP |
由(2)可知:
| QM |
| DP |
| -8k2 |
| 1+2k2 |
| 4k |
| 1+2k2 |
∴
| QM |
| DP |
| -8k2 |
| 1+2k2 |
| 4k |
| 1+2k2 |
即
| 8k2 |
| 1+2k2 |
∴x0=0.
∴存在Q(0,0),使得以MP为直径的圆恒过直线DP、MQ的交点.
点评:本题考查椭圆方程的求法,主要考查了直线与椭圆的位置关系的应用,训练了向量法解决与圆锥曲线有关的问题,直线与曲线联立,根据方程的根与系数的关系解题,是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考试具备较强的运算推理的能力,是高考试卷中的压轴题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
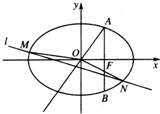 如图,已知椭圆C:
如图,已知椭圆C: