题目内容
以直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点 的直角坐标为
的直角坐标为 ,点
,点 的极坐标为
的极坐标为 ,若直线
,若直线 过点
过点 ,且倾斜角为
,且倾斜角为 ,圆
,圆 以
以 为 圆心、
为 圆心、 为半径.
为半径.
(1)求直线 的参数方程和圆
的参数方程和圆 的极坐标方程;
的极坐标方程;
(2)试判定直线 和圆
和圆 的位置关系.
的位置关系.
(1) ,
, ;(2)相离.
;(2)相离.
解析试题分析:(1)由若直线 过点
过点 ,且倾斜角为
,且倾斜角为 ,
, 的直角坐标为
的直角坐标为 ,可得直线
,可得直线 的参数方程,由圆
的参数方程,由圆 以
以 为 圆心、
为 圆心、 为半径,
为半径, 的极坐标为
的极坐标为 可得圆
可得圆 的极坐标方程;(2)先将直线
的极坐标方程;(2)先将直线 的参数方程,与圆的极坐标方程转化为平面直角坐标系下的方程,利用圆心到直线的距离与半径的关系判断直线与圆的关系.
的参数方程,与圆的极坐标方程转化为平面直角坐标系下的方程,利用圆心到直线的距离与半径的关系判断直线与圆的关系.
试题解析:
解(1) -3分
-3分 -6分
-6分
(2) ,
,
 -10分
-10分 -12分
-12分
考点:参数方程,极坐标方程与平面直角坐标系下的方程的转化,点到直线的距离公式.

练习册系列答案
相关题目
 :
: (
( 为参数),
为参数), :
: (
( 为参数).
为参数). 对应的参数为
对应的参数为 ,
, 为
为 中点
中点 到直线
到直线 :
: (
( ρ·cos
ρ·cos +6=0.
+6=0. ,
, .
. 垂直,根据(1)中你得到的参数方程,确定D的坐标.
垂直,根据(1)中你得到的参数方程,确定D的坐标. 的极坐标方程是
的极坐标方程是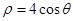 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴正方向建立平面直角坐标系,直线l的参数方程是
轴正方向建立平面直角坐标系,直线l的参数方程是 (
( 为参数).
为参数). 、
、 两点,点
两点,点 的直角坐标为(2,1),若
的直角坐标为(2,1),若 ,求直线l的普通方程.
,求直线l的普通方程. 的极坐标方程为
的极坐标方程为 ,直线
,直线 的参数方程为
的参数方程为
 为参数),点
为参数),点 的极坐标为
的极坐标为 ,设直线
,设直线 .
. 的值.
的值. 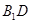 的圆心为
的圆心为 ,半径为
,半径为 ,点
,点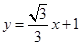 为圆
为圆 上异于极点
上异于极点 的动点,求弦
的动点,求弦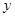 中点的轨迹的极坐标方程.
中点的轨迹的极坐标方程. .
. 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线 ,求|MA|·|MB|.
,求|MA|·|MB|. 到直线
到直线 的距离等于
的距离等于