题目内容
已知曲线 的极坐标方程是
的极坐标方程是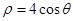 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴正方向建立平面直角坐标系,直线l的参数方程是
轴正方向建立平面直角坐标系,直线l的参数方程是 (
( 为参数).
为参数).
(1)求曲线 的直角坐标方程;
的直角坐标方程;
(2)设直线l与曲线 交于
交于 、
、 两点,点
两点,点 的直角坐标为(2,1),若
的直角坐标为(2,1),若 ,求直线l的普通方程.
,求直线l的普通方程.
(1) ;(2)
;(2) 或
或
解析试题分析:(1)由曲线 的极坐标方程是
的极坐标方程是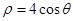 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴正方向建立平面直角坐标系,在极坐标方程两边同乘以
轴正方向建立平面直角坐标系,在极坐标方程两边同乘以 ,根据极坐标与普通方程相互转化的等式关系可得求曲线
,根据极坐标与普通方程相互转化的等式关系可得求曲线 的直角坐标方程.
的直角坐标方程.
(2)直线l与曲线 交于
交于 、
、 两点,点
两点,点 的直角坐标为(2,1),若
的直角坐标为(2,1),若 ,所以
,所以 .即直线方程与圆的方程联立即可得到一个关于t的方程,再由
.即直线方程与圆的方程联立即可得到一个关于t的方程,再由 以及韦达定理即可得到结论.
以及韦达定理即可得到结论.
(1)由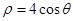 ,得
,得 ,
,
 ,
,
 曲线
曲线 的直角坐标方程是
的直角坐标方程是 ,即
,即 . 3分
. 3分
(2)设 ,
, ,
,
由已知 ,得
,得 ① 4分
① 4分
联立直线的参数方程与曲线 的直角坐标方程得:
的直角坐标方程得: ,
,
整理得: ,
, ,与①联立得:
,与①联立得: ,
,
 直线的参数方程为
直线的参数方程为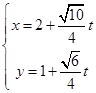 (
( 为参数)或
为参数)或 (
( 为参数)
为参数)
消去参数的普通方程为 或
或 7分
7分
考点:1.极坐标方程.2.参数方程.3.直线与圆的位置关系.

练习册系列答案
相关题目
 sin
sin ,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线
,以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为 (t为参数),判断直线
(t为参数),判断直线 (
( >0),已知过点P(-2,-4)的直线l的参数方程为:
>0),已知过点P(-2,-4)的直线l的参数方程为: (t为参数),直线l与曲线C分别交于M,N两点.
(t为参数),直线l与曲线C分别交于M,N两点. 为极点,
为极点, 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点 的直角坐标为
的直角坐标为 ,点
,点 的极坐标为
的极坐标为 ,若直线
,若直线 过点
过点 ,圆
,圆 以
以 为半径.
为半径. 轴的正半轴为极轴建立极坐极系,并在两种坐极系中取相同的长度单位.已知直线的极坐标方程为
轴的正半轴为极轴建立极坐极系,并在两种坐极系中取相同的长度单位.已知直线的极坐标方程为 (
( ),它与曲线
),它与曲线 (
( 为参数)相交于两点A和B,求AB的长.
为参数)相交于两点A和B,求AB的长.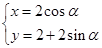 (
( 为参数)M是C1上的动点,P点满足
为参数)M是C1上的动点,P点满足 ,P点的轨迹为曲线C2
,P点的轨迹为曲线C2 与C1的异于极点的交点为A,与C2的异于极点的交点为B,求
与C1的异于极点的交点为A,与C2的异于极点的交点为B,求 .
. ,点F1,F2为其左、右焦点,直线l的参数方程为
,点F1,F2为其左、右焦点,直线l的参数方程为 (t为参数,t∈R).
(t为参数,t∈R). ,
, ,那么顶点
,那么顶点 的坐标可能是
的坐标可能是