题目内容
已知圆的极坐标方程为ρ2－4
ρ·cos
＋6＝0.
(1)将极坐标方程化为普通方程，并选择恰当的参数写出它的参数方程；
(2)若点P(x，y)在该圆上，求x＋y的最大值和最小值．
（1）普通方程：
，圆的参数方程为：
，
为参数；
（2）
.
解析试题分析：（1）圆的普通方程与圆的极坐标方程之间的转换关系在于圆上一点
与极径
，极角间的关系：
,圆的普通方程与圆的参数方程的关系也在于此，即圆上一点与圆半径
,圆上点与圆心
连线与
轴正向夹角的关系：
；（2）利用圆的参数方程，将
转化为关于的三角函数关系求最值，一般将三角函数转化为
的形式.
试题解析：
由圆上一点与极径，极角间的关系：，可得
,
并可得圆的标准方程：
,
所以得圆的参数方程为：，为参数.
由（1）可知：
故.
考点：(1)圆的普通方程与圆的参数方程和极坐标之间的关系；（2）利用参数方程求最值.
练习册系列答案
阅读快车系列答案
相关题目
sin
，以极点为坐标原点，极轴为x轴的正半轴建立平面直角坐标系，直线
的参数方程为
(t为参数)，判断直线
轴正半轴．已知曲线
的极坐标方程为
，曲线
的参数方程为
（其中
为参数）
的直角坐标方程和曲线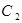
的普通方程；
(
>0),已知过点P(-2,-4)的直线l的参数方程为:
（t为参数）,直线l与曲线C分别交于M,N两点．
为极点，
轴的正半轴为极轴，已知点
的直角坐标为
，点
的极坐标为
，若直线
过点
，圆
以
为半径.
（
为参数）M是C1上的动点，P点满足
,P点的轨迹为曲线C2
与C1的异于极点的交点为A，与C2的异于极点的交点为B，求
.
围成的面积是 
轴的正半轴为极轴，并在两种坐标系中取相同的长度单位。已知直线的极坐标方程为
，它与曲线
（
为参数）相交于两点A和B，则|AB|=_______.