题目内容
已知圆
的极坐标方程为
，直线
的参数方程为
（
为参数），点
的极坐标为
，设直线与圆交于点
、
.
（1）写出圆的直角坐标方程；
（2）求
的值.
（1）
；（2）
.
解析试题分析：（1）在极坐标方程的两边同时乘以
，然后由
，
即可得到圆的直角坐标方程；（2）将直线的标准参数方程代入圆的直角坐标方程，消去
、
得到有关的参数方程，然后利用韦达定理求出的值.
（1）由，得
，，
即，
即圆的直角坐标方程为；
（2）由点的极坐标得点直角坐标为
，
将
代入消去、，整理得
，
设
、
为方程的两个根，则
，
所以
.
考点：1.圆的极坐标方程与直角坐标方程之间的转化；2.韦达定理
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
轴正半轴．已知曲线
的极坐标方程为
，曲线
的参数方程为
（其中
为参数）
的直角坐标方程和曲线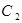
的普通方程；
为极点，
轴的正半轴为极轴，已知点
的直角坐标为
，点
的极坐标为
，若直线
过点
，圆
以
为半径.
的直角坐标方程为
. 以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系. P是曲线
，
，将点P绕点O逆时针旋转角
后得到点Q，
，点M的轨迹是曲线
.
的取值范围.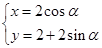
（
为参数）M是C1上的动点，P点满足
,P点的轨迹为曲线C2
与C1的异于极点的交点为A，与C2的异于极点的交点为B，求
.
为圆心，1为半径的圆的极坐标方程是 ．
(t为参数)相交于A、B两点，求|AB|.
，求|CP|.
＝2
.
(t∈R为参数)，求a，b的值．