题目内容
5.定积分(${∫}_{\frac{-π}{3}}^{\frac{π}{3}}$(2x+sinx)dx等于( )| A. | 0 | B. | $\frac{π^2}{9}-\frac{1}{2}$ | C. | $\frac{{2{π^2}}}{9}-1$ | D. | $\frac{{2{π^2}}}{9}+1$ |
分析 根据定积分的计算法则计算即可.
解答 解:${∫}_{\frac{-π}{3}}^{\frac{π}{3}}$(2x+sinx)dx=(x2-cosx)|${\;}_{-\frac{π}{3}}^{\frac{π}{3}}$=0,
故选:A.
点评 本题考查了定积分的计算,关键是掌握基本初等函数的导数公式,属于基础题.

练习册系列答案
相关题目
17.如果直线3ax-by+15=0(a>0,b>0)和函数f(x)=mx+1+2(m>0,m≠1)的图象恒过同一个定点,且该定点始终落在圆(x-a+1)2+(y+b-3)2=16的内部或圆上,那么,$\frac{a}{b}$的取值范围是( )
| A. | [$\frac{16-5\sqrt{7}}{9}$,$\frac{16+5\sqrt{7}}{9}$) | B. | ($\frac{16-5\sqrt{7}}{9}$,$\frac{16+5\sqrt{7}}{9}$) | C. | [$\frac{16-5\sqrt{7}}{9}$,$\frac{16+5\sqrt{7}}{9}$] | D. | ($\frac{16-5\sqrt{7}}{9}$,$\frac{16+5\sqrt{7}}{9}$] |
15.设函数$f(x)={({\frac{1}{3}})^x}$与g(x)=3-x的图象的交点为( x0,y0 ),则x0所在的区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
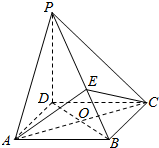 如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,O为AC与BD的交点,E为棱PB上一点,证明:平面EAC⊥平面PBD.
如图所示,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,O为AC与BD的交点,E为棱PB上一点,证明:平面EAC⊥平面PBD.