题目内容
3.函数f(x)=cosx-$\frac{1}{2}$cos2x(x∈R)的最大值等于$\frac{3}{4}$.分析 利用倍角公式及其配方法可得:f(x)=$(cosx-\frac{1}{2})^{2}$+$\frac{3}{4}$,再利用二次函数的单调性即可得出.
解答 解:f(x)=cosx-$\frac{1}{2}$cos2x=cosx-$\frac{1}{2}(2co{s}^{2}x-1)$=$-co{s}^{2}x+cosx+\frac{1}{2}$=-$(cosx-\frac{1}{2})^{2}$+$\frac{3}{4}$,
当cosx=$\frac{1}{2}$时,函数f(x)取得最大值$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查了倍角公式、配方法、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.F为双曲线Г:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,若Г上存在一点P使得△OPF为等边三角形(O为坐标原点),则Г的离心率e为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\sqrt{3}+1$ | D. | 2 |
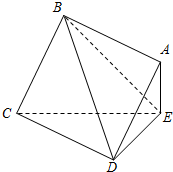 如图,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,
如图,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,