题目内容

12．椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左焦点为F1，对定点M（6，4），若P为椭圆上一点，则|PF1|+|PM|的最大值为15．

分析 由椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1可得：a2=25，b2=16，c=3．由|PM|+|PF1|=2a+|PM|-|PF2|≤2a+|MF2|，当且仅当三点M、F2、P共线时取等号．

解答 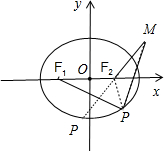解：由椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1焦点在x轴上，可得：a2=25，b2=16．
∴a=5，b=4，c=3．
∴F2（3，0），|MF2|=5．
∴|PM|+|PF1|=2a+|PM|-|PF2|≤2×5+|MF2|=15，
当且仅当三点M、F2、P共线时取等号．
故答案为：15．

点评 本题考查了椭圆的定义标准方程及其性质、最大值问题的转化为三角形的三边关系，属于中档题

练习册系列答案
相关题目
2．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，连接椭圆的四个顶点得到的菱形的面积为4$\sqrt{3}$．
（1）求椭圆C的方程；
（2）已知O为坐标原点，点P是圆C1：x2+y2=$\frac{5}{3}$上的点，过P作圆的切线交椭圆于M，N两点，求△OMN面积的最大值，并求出面积最大值时切线的斜率．
3．已知直线y=x+k与曲线y=ex相切，则k的值为（　　）
A．eB．2C．1D．0
20．点P是抛物线y2=4x上一动点，则点P到点（0，-1）的距离与抛物线准线的距离之和最小时，P的坐标是（3-2$\sqrt{2}$，2-2$\sqrt{2}$）．
7．在平面内，一只蚂蚁从点A（-2，-3）出发，爬到y轴后又爬到圆（x+3）2+（y-2）2=2上，则它爬到的最短路程是（　　）
A．5$\sqrt{2}$B．4$\sqrt{2}$C．$\sqrt{26}$D．$\sqrt{26}$-$\sqrt{2}$
17．设等差数列{an}的前n项和为Sn，已知a2=-10，a3+a7=-8，当Sn取得最小值时，n的值为（　　）
A．5B．6C．7D．6或7
4．直线x-2017=0的倾斜角为（　　）
A．0B．$\frac{π}{3}$C．$\frac{π}{2}$D．不存在
1．已知数列{an}对任意的n∈N*满足：an+2+an＞2an+1，则称数列{an}为“T数列”．
（Ⅰ）求证：数列{2n}是“T数列”；
（Ⅱ）若${a_n}={n^2}•{（{\frac{1}{2}}）^n}$，试判断数列{an}是否是“T数列”，并说明理由；
（Ⅲ）若数列{an}是各项均为正的“T数列”，求证：$\frac{{{a_1}+{a_3}+…+{a_{2n+1}}}}{{{a_2}+{a_4}+…+{a_{2n}}}}＞\frac{n+1}{n}$．
2．如果正方体、球与等边圆柱（圆柱底面圆的直径与高相等）的体积相等，设它们的表面积依次为S1，S2，S3，则S1，S2，S3大小关系为S2＜S3＜S1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网