题目内容
20.在斜△ABC中,内角A,B,C所对的边长分别是a,b,c,asinB+bcos(B+C)=0,sinA+sin(B-C)=2$\sqrt{2}$sin2C,且△ABC的面积为1,则a的值为( )| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
分析 由asinB+bcos(B+C)=0,利用正弦定理可得sinAsinB-sinBcosA=0,由sinB≠0,化为sinA=cosA,A∈(0,π),可得A=$\frac{π}{4}$.
由sinA+sin(B-C)=2$\sqrt{2}$sin2C,利用和差公式、倍角公式展开可得sinB=2$\sqrt{2}$sinC,利用正弦定理可得b=2$\sqrt{2}$c.再利用余弦定理与三角形面积计算公式即可得出.
解答 解:在斜△ABC中,∵asinB+bcos(B+C)=0,
∴sinAsinB-sinBcosA=0,
∵sinB≠0,
∴sinA=cosA,A∈(0,π),
∴tanA=1,解得A=$\frac{π}{4}$.
∵sinA+sin(B-C)=2$\sqrt{2}$sin2C,
∴sinBcosC+cosBsinC+sinBcosC-cosBsinC=2$\sqrt{2}$sin2C,
∴2sinBcosC=4$\sqrt{2}$sinCcosC
∵cosC≠0,
∴sinB=2$\sqrt{2}$sinC,
∴b=2$\sqrt{2}$c.
由余弦定理可得:a2=$(2\sqrt{2}c)^{2}+{c}^{2}$-2×$2\sqrt{2}$c2cos$\frac{π}{4}$=5c2.
∵△ABC的面积为1,
∴$\frac{1}{2}bcsinA$=1,
∴$\frac{1}{2}×2\sqrt{2}{c}^{2}×sin\frac{π}{4}$=1,解得c2=1.
则a=$\sqrt{5}$.
故选:B.
点评 本题考查了正弦定理余弦定理、和差公式、倍角公式、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.函数f(x)=2sin(ωx+φ)(w>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)+f($\frac{17π}{12}$)的值为( )
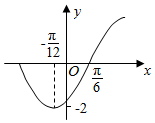
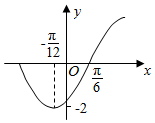
| A. | 2-$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 1-$\frac{\sqrt{3}}{2}$ | D. | 1+$\frac{\sqrt{3}}{2}$ |
5.一个圆过点(-5,1)且圆心在直线2x+y+4=0上,求半径最小时的圆心坐标( )
| A. | (-1,-2) | B. | (-2,0) | C. | (-$\frac{5}{2}$,1) | D. | (-3,2) |
12.已知集合A={x|x2<1},B={x|log2x<1},则A∩B=( )
| A. | {x|-1<x<1} | B. | {x|0<x<1} | C. | {x|0<x<2} | D. | {x|-1<x<2} |

 如图,已知正三棱柱ABC-A1B1C1的体积为$9\sqrt{3}$,底面边长为3,求异面直线BC1与AC所成的角的大小.
如图,已知正三棱柱ABC-A1B1C1的体积为$9\sqrt{3}$,底面边长为3,求异面直线BC1与AC所成的角的大小.