题目内容
在Rt△ABC中，∠A=30°，过直角顶点C作射线CM交线段AB于M，使|AM|＞|AC|的概率是 ．
考点：几何概型
专题：概率与统计
分析：作图，设置线段的长度，作点M恰好使得AM=AC，由几何几何概型可得P=
，代值可得．
| ∠BCM |
| ∠BCA |
解答：
解：如图，不妨设BC=1，则AB=2，AC=
，
图中点M恰好使得AM=AC=
，
∴当点位于BM段时，满足|AM|＞|AC|，
由三角形的知识易得∠BCM=15°
∴使|AM|＞|AC|的概率P=
=
故答案为：
| 3 |
图中点M恰好使得AM=AC=
| 3 |
∴当点位于BM段时，满足|AM|＞|AC|，
由三角形的知识易得∠BCM=15°
∴使|AM|＞|AC|的概率P=
| 15 |
| 90 |
| 1 |
| 6 |
故答案为：
| 1 |
| 6 |
点评：本题考查几何概型，作图是解决问题的关键，属基础题．
练习册系列答案
相关题目
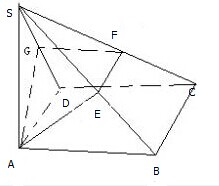已知矩形ABCD，过A作SA⊥平面AC，再过A作AE⊥SB交SB于E，过E作EF⊥SC交SC于F．
如图，曲边梯形ABCD由直线x=1、x=e、x轴及曲线y=