题目内容
2.已知集合A={x|x2-2x-3≤0},B={x|log2(x2-x)>1}则A∩B=( )| A. | (2,3) | B. | (2,3] | C. | (-3,-2) | D. | [-3,-2) |
分析 求出A,B中x的范围确定出A,B,再求出两集合的交集即可.
解答 解:由A中不等式变形得:(x-3)(x+1)≤0,
解得:-1≤x≤3,即A=[-1,3],
由log2(x2-x)>1,得到x2-x-2>0,即x<-1或x>2,
∴B=(-∞,-1)∩(2,+∞),
由B中则A∩B=(2,3],
故选:B.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
10.一个几何体的三视图如图所示,该几何体的体积是( )


| A. | 12 | B. | 18 | C. | 24 | D. | 36 |
7.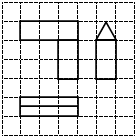 如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为( )
如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为( )
 如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为( )
如图,网格纸的小正方形的边长是1,粗线画出的是一个几何体的三视图,则这个几何体的体积为( )| A. | $\frac{5}{2}$ | B. | $\frac{7}{2}$ | C. | 2+$\frac{\sqrt{3}}{4}$ | D. | 3+$\frac{\sqrt{3}}{3}$ |
18.已知$tanθ=\frac{3}{4}$,那么$tan(θ+\frac{π}{4})$等于( )
| A. | -7 | B. | $-\frac{1}{7}$ | C. | 7 | D. | $\frac{1}{7}$ |