题目内容
18.已知f(x)=1+log2x(1≤x≤4),设函数g(x)=f2(x)+f(x2),则g(x)max-g(x)min=5.分析 换元t=log2x,求得0≤t≤1,化简g(x)即为h(t)=t2+4t+2,0≤t≤1,求出对称轴t=-2,可得h(t)在[0,1]为增函数,计算即可得答案.
解答 解:∵f(x)=1+log2x(1≤x≤4),
∴$\left\{\begin{array}{l}{1≤x≤4}\\{1≤{x}^{2}≤4}\end{array}\right.$,即1≤x≤2,
∵f(x)=1+log2x(1≤x≤4),
g(x)=f2(x)+f(x2)=(1+log2x)2+1+2log2x,
∴g(x)=(log2x)2+4log2x+2,1≤x≤2
设t=log2x,则h(t)=t2+4t+2,0≤t≤1,
∵对称轴t=-2,h(t)在[0,1]为增函数,
∴g(x)的最小值为h(0)=2,最大值为h(1)=7
则g(x)max-g(x)min=7-2=5.
故答案为:5.
点评 本题考查函数的最值的求法,注意运用换元法转化为二次函数求值域问题,注意自变量的范围,同时考查对数函数的单调性的运用,属于中档题和易错题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
6.设向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为θ,则“$\overrightarrow{a}$•$\overrightarrow{b}$<0”是“θ为钝角”的( )
| A. | 充分不必要条件 | B. | 必要不充分 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
3.已知数列{an}为等差数列,Sn为前n项和,公差为d,若$\frac{{S}_{2017}}{2017}$-$\frac{{S}_{17}}{17}$=100,则d的值为( )
| A. | $\frac{1}{20}$ | B. | $\frac{1}{10}$ | C. | 10 | D. | 20 |
10.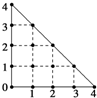 某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如表所示:
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如表所示:
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(1)完成下表,并求所种作物的平均年收获量:
(2)在所种年收获量为51或48的作物中随机选取两株求收获量之和,收获量之和为t的概率.
 某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如表所示:
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如表所示:| X | 1 | 2 | 3 | 4 |
| Y | 51 | 48 | 45 | 42 |
(1)完成下表,并求所种作物的平均年收获量:
| Y | 51 | 48 | 45 | 42 |
| 频数 |
