题目内容
5．在平面四边形ABCD中，连接对角线BD，已知CD=9，BD=16，∠BDC=90°，sinA=$\frac{4}{5}$，则对角线AC的最大值为27．分析 根据题意，建立坐标系，求出D、C、B的坐标，设ABD三点都在圆E上，其半径为R，由正弦定理计算可得R=10，进而分析可得E的坐标，由于sinA为定值，则点A在以点E（-6，8）为圆心，10为半径的圆上，当且仅当C、E、A三点共线时，AC取得最大值，计算即可得答案．
解答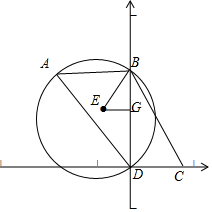 
解：根据题意，建立如图的坐标系，则D（0，0），C（9，0），B（0，16），BD中点为G，则G（0，8），
设ABD三点都在圆E上，其半径为R，
在Rt△ADB中，由正弦定理可得$\frac{a}{sinA}$=$\frac{16}{\frac{4}{5}}$=2R=20，即R=10，
即EB=10，BG=8，则EG=6，
则E的坐标为（-6，8），
故点A在以点E（-6，8）为圆心，10为半径的圆上，
当且仅当C、E、A三点共线时，AC取得最大值，此时AC=10+EC=27；
故答案为：27．
点评 本题考查正弦定理的应用，注意A为动点，需要先分析A所在的轨迹．
练习册系列答案
相关题目
13．若将函数y=3cos（2x+$\frac{π}{2}$）的图象向右平移$\frac{π}{6}$个单位长度，则平移后图象的一个对称中心是（ ）
| A． | （$\frac{π}{6}$，0） | B． | （-$\frac{π}{6}$，0） | C． | （$\frac{π}{12}$，0） | D． | （-$\frac{π}{12}$，0） |
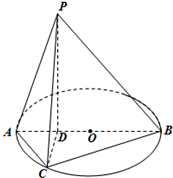如图，已知PD垂直于以AB为直径的圆O所在的平面，点D在线段AB上，点C为圆O上一点，且BD=PD=3，AC=2AD=2．