题目内容
已知函数 .
.
(Ⅰ)请用“五点法”画出函数 在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);
在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);

(Ⅱ)求函数 的单调递增区间;
的单调递增区间;
(Ⅲ)当 时,求函数
时,求函数 的最大值和最小值及相应的
的最大值和最小值及相应的 的值.
的值.
(I)过程见解析;(Ⅱ)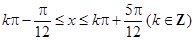 ;(Ⅲ)当x=0时,函数取得最小值
;(Ⅲ)当x=0时,函数取得最小值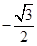 ;当x=
;当x=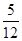 p时,函数取得最大值1.
p时,函数取得最大值1.
解析试题分析:(I)画三角函数图象的方法是五点法,具体步骤是1.列表,标出一个周期内与x轴的交点和最大值点与最小值点;2.描点,将列出的5个点画在平面直角坐标系中;3.连线,用平滑的曲线连接5点;由题,列表如下,描点连线; (Ⅱ)三角函数sinx在[-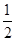 p,
p,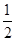 p]上递增,在[
p]上递增,在[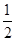 p,
p,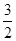 p]上递减,由题,令
p]上递减,由题,令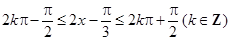 ,可解得
,可解得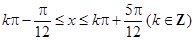 ,故函数f(x)在
,故函数f(x)在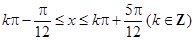 递增;(Ⅲ)由x的范围可以得到2x-
递增;(Ⅲ)由x的范围可以得到2x-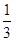 p的范围,再由(Ⅱ)中函数的增减性可以求得最大值和最小值.
p的范围,再由(Ⅱ)中函数的增减性可以求得最大值和最小值.
试题解析:(I)令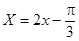 ,则
,则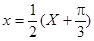 .填表:
.填表: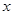
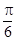
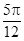
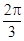
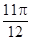
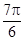
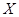
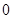
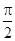
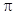
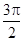
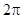
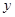
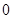
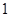
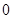
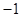
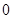
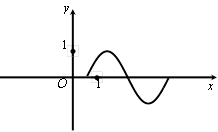
(Ⅱ)令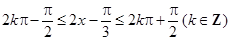 ,
,
解得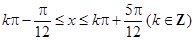 ,
,
∴函数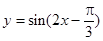 的单调增区间为
的单调增区间为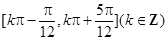 .
.
(Ⅲ)∵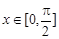

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
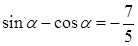 .求
.求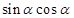 和
和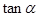 的值.
的值.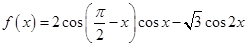 ,
,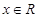 .
.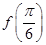 的值;
的值;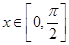 时,求
时,求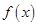 的最值.
的最值. .
.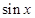 的值;
的值;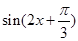 的值.
的值.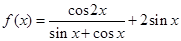 .
.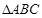 中,
中,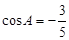 ,求
,求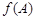 的值;
的值;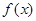 的最小正周期及其图象的所有对称轴的方程.
的最小正周期及其图象的所有对称轴的方程.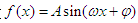 (其中
(其中 )的图象如图所示,把函数
)的图象如图所示,把函数 的图像向右平移
的图像向右平移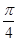 个单位,再向下平移1个单位,得到函数
个单位,再向下平移1个单位,得到函数 的图像.
的图像.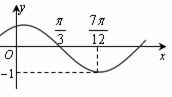
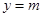 与函数
与函数 图像在
图像在 时有两个公共点,其横坐标分别为
时有两个公共点,其横坐标分别为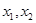 ,求
,求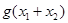 的值;
的值; 内角
内角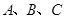 的对边分别为
的对边分别为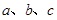 ,且
,且
 .若向量
.若向量 与
与 共线,求
共线,求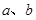 的值.
的值. 在R上的最大值为5.
在R上的最大值为5. 的单调递减区间。
的单调递减区间。 ,已知
,已知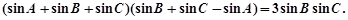
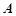 值;
值; 的最大值.
的最大值.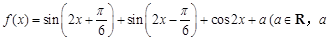 为常数).
为常数).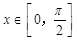 时,
时,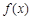 的最小值为– 2 ,求a的值.
的最小值为– 2 ,求a的值.