题目内容
18.已知函数f(x)=2$\sqrt{3}$sin(π+x) cos(-3π-x)-2sin($\frac{π}{2}$-x)cos(π-x).(1)求函数f(x)的单调递增区间;
(2)若f($\frac{α}{2}$-$\frac{π}{12}$)=$\frac{3}{2}$,α是第二象限角,求cos(2α+$\frac{π}{3}$)的值.
分析 (1)利用诱导公式和辅助角公式将已知函数解析式转化为正弦函数,结合正弦函数图象来求其单调递增区间;
(2)由(1)中的函数解析式求得sinα=$\frac{1}{4}$.根据α的取值范围得到cosα=-$\frac{\sqrt{15}}{4}$.所以利用二倍角公式和两角和与差的余弦公式进行解答即可.
解答 解:(1)f(x)=$\sqrt{3}$sin2x-2cosx(-cosx)=$\sqrt{3}$sin2x+2cos2x=$\sqrt{3}$sin2x+cos2x+1=2sin(2x+$\frac{π}{6}$)+1,
由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$(k∈Z),得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$(k∈Z).
故函数f(x)的单调增区间为[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z).
(2)∵f($\frac{α}{2}$-$\frac{π}{12}$)=2sinα+1=$\frac{3}{2}$,
∴sinα=$\frac{1}{4}$.
∵α是第二象限角,
∴cosα=-$\sqrt{1-sin2α}$=-$\frac{\sqrt{15}}{4}$.
∴sin2α=-$\frac{\sqrt{15}}{8}$,cos2α=$\frac{7}{8}$.
∴cos(2α+$\frac{π}{3}$)=cos2αcos$\frac{π}{3}$-sin2αsin$\frac{π}{3}$=$\frac{7}{8}$×$\frac{1}{2}$-(-$\frac{\sqrt{15}}{8}$)×$\frac{\sqrt{3}}{2}$=$\frac{7+3\sqrt{5}}{16}$.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.

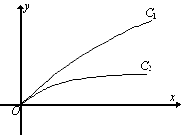 如图,当参数λ=λ1,λ2时,连续函数y=$\frac{x}{1+λx}$(x≥0)的图象分别对应曲线C1和C2,则( )
如图,当参数λ=λ1,λ2时,连续函数y=$\frac{x}{1+λx}$(x≥0)的图象分别对应曲线C1和C2,则( )| A. | 0<λ2<λ1 | B. | λ2<λ1<0 | C. | λ1<λ2<0 | D. | 0<λ1<λ2 |
| A. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 | B. | y=x0与g(x)=$\frac{1}{{x}^{0}}$ | ||
| C. | f(x)=|x|,g(x)=$\sqrt{{x}^{2}}$ | D. | f(x)=$\sqrt{x+1}$•$\sqrt{x-1}$,g(x)=$\sqrt{{x}^{2}-1}$ |