题目内容
求y=
的导数.
| 3 | ax2+bx+c |
考点:导数的运算
专题:计算题
分析:先将函数解析式化为指数的形式,利用求导公式和复合函数的求导公式进行化简.
解答:
解:由题意得,y=
=(ax2+bx+c)
,
所以y′=
(ax2+bx+c)
-1•(ax2+bx+c)′
=
(2ax+b)(ax2+bx+c)-
=
.
| 3 | ax2+bx+c |
| 1 |
| 3 |
所以y′=
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 3 |
| 2 |
| 3 |
| 2ax+b | |||
3
|
点评:本题考查基本初等函数的求导公式,以及复合函数的求导公式,熟练掌握公式是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
在等比数列{an}中,a2a3a7=8,则a4=( )
| A、1 | ||
| B、4 | ||
| C、2 | ||
D、2
|
已知角α的顶点为坐标原点,始边为x轴正半轴,终边经过点(-4,3),则cosα=( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知集合A={x|x≤1},B={x|x2-2x<0}.则A∩B=( )
| A、(0,1] |
| B、[1,2) |
| C、(0,1) |
| D、(0,2) |
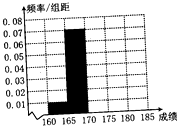 某校在自主招生考试成绩中随机抽取100名学生的笔试成绩,被抽取学生的成绩均不低于160分,且低于185分,如图是按成绩分组得到的频率分布图的一部分(每一组均包括左端点数据),且第三组、第四组、第五组的频数之比一次为3:2:1.
某校在自主招生考试成绩中随机抽取100名学生的笔试成绩,被抽取学生的成绩均不低于160分,且低于185分,如图是按成绩分组得到的频率分布图的一部分(每一组均包括左端点数据),且第三组、第四组、第五组的频数之比一次为3:2:1.