题目内容
18.若动直线x=t(t∈R)与函数f(x)=cos2($\frac{π}{4}$-x),g(x)=$\sqrt{3}$sin($\frac{π}{4}$+x)cos($\frac{π}{4}$+x)的图象分别交于P、Q两点,则线段PQ长度的最大值为$\frac{3}{2}$.分析 利用三角函数的二倍角公式化简f(x)和g(x),|PQ|=|f(t)-g(t)|,即求=|f(t)-g(t)|的最大值.
解答 解:函数f(x)=cos2($\frac{π}{4}$-x)=$\frac{1}{2}$$+\frac{1}{2}$cos($\frac{π}{2}-2x$)=$\frac{1}{2}$sin2x+$\frac{1}{2}$;
函数g(x)=$\sqrt{3}$sin($\frac{π}{4}$+x)cos($\frac{π}{4}$+x)=$\frac{\sqrt{3}}{2}$sin(2x+$\frac{π}{2}$)=$\frac{\sqrt{3}}{2}$cos2x.
由题意,|PQ|=|f(t)-g(t)|,即|PQ|=$\frac{1}{2}$sin2t+$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$cos2t|=|sin(2t-$\frac{π}{3}$)$+\frac{1}{2}$|.
当sin(2t-$\frac{π}{3}$)取得最大值时,可得|PQ|的最大值.
∴|PQ|的最大值为1+$\frac{1}{2}$=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查了三角函数的二倍角公式化简计算能力和三角函数图象性质的运用,属于中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
4.运行如下程序框图,如果输入的t∈[0,5],则输出S属于( )
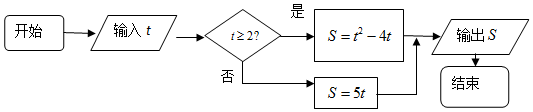

| A. | [-4,10) | B. | [-5,2] | C. | [-4,3] | D. | [-2,5] |
5.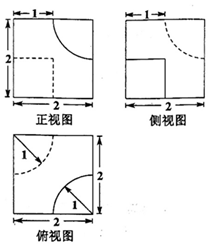 如图所示某物体的三视图,则求该物体的体积为( )
如图所示某物体的三视图,则求该物体的体积为( )
 如图所示某物体的三视图,则求该物体的体积为( )
如图所示某物体的三视图,则求该物体的体积为( )| A. | $8-\frac{5π}{12}$ | B. | $8-\frac{π}{3}$ | C. | $8-\frac{π}{2}$ | D. | $8-\frac{7π}{12}$ |
3.已知以O为中心的双曲线C的一个焦点为F,P为C上一点,M为PF的中点,若△OMF为等腰直角三角形,则C的离心率等于( )
| A. | $\sqrt{2}-1$ | B. | $\sqrt{2}+1$ | C. | $2+\sqrt{2}$ | D. | $\frac{\sqrt{5}+1}{2}$ |
10.如图是一个几何体的三视图,则该几何体的体积为( )
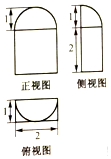

| A. | 2+π | B. | $3+\frac{π}{2}$ | C. | 3+π | D. | $4+\frac{π}{3}$ |