题目内容
已知f(x+1)=f(x-1),f(x)=f(-x+2),方程f(x)=0在[0,1]内有且只有一个根
,则f(x)=0在区间[0,2014]内根的个数为( )
| 1 |
| 2 |
| A、1006 | B、1007 |
| C、2013 | D、2014 |
考点:根的存在性及根的个数判断
专题:计算题,函数的性质及应用
分析:由题意可推出f(x)=0的根为x=k+
,k∈Z;从而得到f(x)=0在区间[0,2014]内根的个数.
| 1 |
| 2 |
解答:
解:∵f(x)=f(-x+2),
∴f(x)的图象关于x=1对称,
又∵方程f(x)=0在[0,1]内有且只有一个根
,
∴方程f(x)=0在[1,2]内有且只有一个根
,
故方程f(x)=0在[0,2]上有且只有两个根
,
;
又∵f(x+1)=f(x-1),
∴f(x)是周期为2的函数,
故f(x)=0的根为x=k+
,k∈Z;
故f(x)=0在区间[0,2014]内根的个数为2013,
故选C.
∴f(x)的图象关于x=1对称,
又∵方程f(x)=0在[0,1]内有且只有一个根
| 1 |
| 2 |
∴方程f(x)=0在[1,2]内有且只有一个根
| 3 |
| 2 |
故方程f(x)=0在[0,2]上有且只有两个根
| 1 |
| 2 |
| 3 |
| 2 |
又∵f(x+1)=f(x-1),
∴f(x)是周期为2的函数,
故f(x)=0的根为x=k+
| 1 |
| 2 |
故f(x)=0在区间[0,2014]内根的个数为2013,
故选C.
点评:本题考查了函数的性质的判断与应用,属于中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知集合M={a,b},N={b,c},则M∩N=( )
| A、{a,b} | B、{b,c} |
| C、{a,c} | D、{b} |
已知F1,F2分别为双曲线
-
=1(a>0,b>0)的左右焦点,如果双曲线上存在一点P,使得F2关于直线PF1的对称点恰在y轴上,则该双曲线的离心率e的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、e>
| ||||
B、1<e<
| ||||
C、e>
| ||||
D、1<e<
|
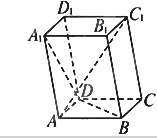 已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形.AA1=2,∠A1AB=∠A1AD=120°.
已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形.AA1=2,∠A1AB=∠A1AD=120°.