Question

2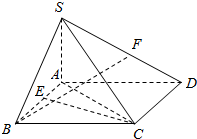．如图，在四棱锥S-ABCD中，SA=SB，底面ABCD是菱形，且∠ABC=60°，点E、F分别是AB、SD的中点．
（1）证明：平面SAB⊥平面SEC；
（2）若BC=2，SE=3，平面SAB⊥底面ABCD，求三棱锥F-AEC的体积．

Answer 1

分析 （1）证明AB⊥平面SEC，利用平面与平面垂直的判定定理，证明平面SAB⊥平面SEC；
（2）证明SE⊥底面ABCD，F到平面AEC的距离为$\frac{3}{2}$，利用体积公式，即可求三棱锥F-AEC的体积．

解答 （1）证明：∵SA=SB，点E是AB的中点，
∴SE⊥AB，
∵底面ABCD是菱形，且∠ABC=60°，点E是AB的中点，
∴AB⊥CE，
∵SE∩CE=E，
∴AB⊥平面SEC，
∵AB?平面SAB，
∴平面SAB⊥平面SEC；
（2）解：∵平面SAB⊥底面ABCD，平面SAB∩底面ABCD=AB，SE⊥AB，
∴SE⊥底面ABCD，
∵SE=3，F是SD的中点，
∴F到平面AEC的距离为$\frac{3}{2}$，
∵BC=2，
∴S_△AEC=$\frac{1}{2}•1•\sqrt{3}$=$\frac{\sqrt{3}}{2}$，
∴三棱锥F-AEC的体积V=$\frac{1}{3}•\frac{\sqrt{3}}{2}•\frac{3}{2}$=$\frac{\sqrt{3}}{4}$．

点评 本题考查线面垂直，平面与平面垂直的判定与性质，考查三棱锥F-AEC的体积，考查学生分析解决问题的能力，正确运用线面垂直，平面与平面垂直的判定与性质是关键．