题目内容
11.由动点P引圆O:x2+y2=4的两条切线PA,PB,切点分别为A、B,若∠APB=90°.(1)求点P的轨迹方程;
(2)直线l:mx-y+1=0与圆O的交点为M、N,求MN的中点Q的轨迹方程.
分析 (1)直接由圆与切线的平面几何性质求得动点P到原点O的距离为定值$2\sqrt{2}$,则点P的轨迹方程可求;
(2)设出M、N、Q的坐标,把M、N的坐标代入圆的方程,利用点差法得到MN所在直线的斜率,再由弦中点及直线所过定点求斜率,由斜率相等得答案.
解答 解:(1)由圆与切线的平面几何性质知,∠APO=45°,
∵OA⊥AP,∴OP=$\sqrt{2}OA=2\sqrt{2}$,
故P点的轨迹是以O为圆心,以$2\sqrt{2}$为半径的圆,方程为x2+y2=8;
(2)直线l:mx-y+1=0过定点(0,1),
设M(x1,y1)、N(x2,y2),Q(x,y),
则${{x}_{1}}^{2}+{{y}_{1}}^{2}=4$ ①,
${{x}_{2}}^{2}+{{y}_{2}}^{2}=4$ ②,
①-②得:$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}=-\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}=-\frac{x}{y}$(x1≠x2),
即$\frac{y-1}{x-0}=-\frac{x}{y}$(x,y≠0),
整理得:${x}^{2}+(y-\frac{1}{2})^{2}=\frac{1}{4}$(x,y≠0).
验证点(0,0)(0,1)满足题意,
∴MN的中点Q的轨迹方程为${x}^{2}+(y-\frac{1}{2})^{2}=\frac{1}{4}$.
点评 本题考查轨迹方程的求法,训练了“点差法”,涉及弦中点问题,常采用此法,属中档题.

练习册系列答案
相关题目
6.有60件产品,编号为01至60,现从中抽取5件检验,用系统抽样的方法所确定的抽样编号是( )
| A. | 5,10,15,20,25 | B. | 5,12,31,39,57 | C. | 5,17,29,41,53 | D. | 5,15,25,35,45 |
3.平移坐标轴,将坐标原点移至O′(1,-1),则点(-2,0)在新的坐标系的坐标为( )
| A. | (1,-1) | B. | (-2,0) | C. | (-3,1) | D. | (-1,1) |
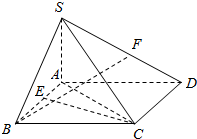 如图,在四棱锥S-ABCD中,SA=SB,底面ABCD是菱形,且∠ABC=60°,点E、F分别是AB、SD的中点.
如图,在四棱锥S-ABCD中,SA=SB,底面ABCD是菱形,且∠ABC=60°,点E、F分别是AB、SD的中点.