题目内容
12.设集合A={y|y=ln[kx2-(k+3)x-1],x∈R},集合B={y|y=x-$\frac{1}{x}$,x∈R},若A=B,则k的取值范围是[0,+∞).分析 对于集合B:f(x)=x-$\frac{1}{x}$(x≠0),f′(x)=1+$\frac{1}{{x}^{2}}$>0,利用单调性可得:其值域为R.因此集合A=R.对于集合A:k=0时化为g(x)=ln(-3x-1),要求-3x-1>0,解得$x<-\frac{1}{3}$,此时g(x)的值域为R,满足题意.k≠0,由$\left\{\begin{array}{l}{k>0}\\{△=(k+3)^{2}+4k>0}\end{array}\right.$解得:k>0,此时函数的值域为R.即可得出.
解答 解:对于集合B:f(x)=x-$\frac{1}{x}$(x≠0),f′(x)=1+$\frac{1}{{x}^{2}}$>0,∴函数f(x)在(-∞,0),(0,+∞)上单调递增.其值域为R.
∵A=B,因此集合A=R.
对于集合A:k=0时化为g(x)=ln(-3x-1),要求-3x-1>0,解得$x<-\frac{1}{3}$,此时g(x)的值域为R,满足题意.
k≠0,由$\left\{\begin{array}{l}{k>0}\\{△=(k+3)^{2}+4k>0}\end{array}\right.$解得:k>0,此时函数的值域为R.
综上可得:k的取值范围是[0,+∞).
故答案为:[0,+∞).
点评 本题考查了利用导数研究函数的单调性值域、集合相等、一元二次不等式的解集与判别式的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.平移坐标轴,将坐标原点移至O′(1,-1),则点(-2,0)在新的坐标系的坐标为( )
| A. | (1,-1) | B. | (-2,0) | C. | (-3,1) | D. | (-1,1) |
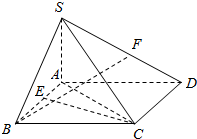 如图,在四棱锥S-ABCD中,SA=SB,底面ABCD是菱形,且∠ABC=60°,点E、F分别是AB、SD的中点.
如图,在四棱锥S-ABCD中,SA=SB,底面ABCD是菱形,且∠ABC=60°,点E、F分别是AB、SD的中点.