题目内容
已知函数f(x)=4x+m·2x+1有且仅有一个零点,求m的取值范围,并求出该零点.
思路分析 由题意可知,方程4x+m·2x+1=0仅有一个实根,再利用换元法求解.
解析 ∵f(x)=4x+m·2x+1有且仅有一个零点,
即方程(2x)2+m·2x+1=0仅有一个实根.
设2x=t(t>0),则t2+mt+1=0.
当Δ=0时,即m2-4=0,
∴m=-2时,t=1;m=2时,t=-1(不合题意,舍去),
∴2x=1,x=0符合题意.
当Δ>0时,即m>2或m<-2时,
t2+mt+1=0有两正或两负根,
即f(x)有两个零点或没有零点.
∴这种情况不符合题意.
综上可知:m=-2时,f(x)有唯一零点,该零点为x=0.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 零点的个数为 .
零点的个数为 .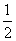 x2+2x+20(万元).一万件售价是20万元,为获取更大利润,该企业一个月应生产该商品数量为( )
x2+2x+20(万元).一万件售价是20万元,为获取更大利润,该企业一个月应生产该商品数量为( )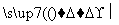 密文
密文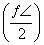 +f2
+f2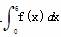 =8,则
=8,则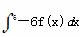 x=( )
x=( )