题目内容
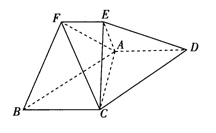
【题目】如图,已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,且∠DAB=90°,∠ABC=45°,CB= ![]() ,AB=2,PA=1.
,AB=2,PA=1. 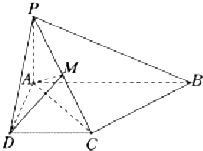
(1)求证:BC⊥平面PAC;
(2)若M是PC的中点,求二面角M﹣AD﹣C的大小.
【答案】
(1)证明:∵PA⊥平面ABCD,∴PA⊥BC,
在△ABC中,由余弦定理可得:AC2= ![]() ﹣2×
﹣2× ![]() =2,
=2,
∴AC2+BC2=AB2=4,
∴∠ACB=90°,即AC⊥BC,
又PC∩AC=A,∴BC⊥平面PAC
(2)解:由(1)可得:AD=CD=1,分别以AD,AB,AP为x,y,z轴,建立空间直角坐标系.
则A(0,0,0),D(1,0,0),P(0,0,1),C(1,1,0),M( ![]() ,
, ![]() ,
, ![]() ),取平面ACD的法向量
),取平面ACD的法向量 ![]() =
= ![]() =(0,0,1).
=(0,0,1).
设平面ADM的法向量为 ![]() =(x,y,z),
=(x,y,z), ![]() =(
=( ![]() ,
, ![]() ,
, ![]() ),
), ![]() =(1,0,0).
=(1,0,0).
由  ,得
,得 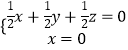 ,取
,取 ![]() =(0,1,﹣1).
=(0,1,﹣1).
cos ![]() =
= ![]() =
= ![]() ,
,
设二面角M﹣AD﹣C的大小为θ,易知θ为锐角.∴cosθ= ![]() ,θ=45°.
,θ=45°.
∴二面角M﹣AD﹣C的大小为45°.

【解析】(1)由PA⊥平面ABCD,可得PA⊥BC.在△ABC中,由余弦定理可得:AC2=2,因此AC2+BC2=AB2 , 可得AC⊥BC,即可证明BC⊥平面PAC.(2)由(1)可得:AD=CD=1,分别以AD,AB,AP为x,y,z轴,建立空间直角坐标系.取平面ACD的法向量 ![]() =
= ![]() =(0,0,1).设平面ADM的法向量为
=(0,0,1).设平面ADM的法向量为 ![]() =(x,y,z),由
=(x,y,z),由  ,可得
,可得 ![]() .利用cos
.利用cos ![]() =
= ![]() ,即可得出.
,即可得出.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.