Question

【题目】已知具有相关关系的两个变量之间的几组数据如下表所示：

（1）请根据上表数据在网格纸中绘制散点图；

（2）请根据上表提供的数据，用最小二乘法求出关于的线性回归方程，并估计当时， 的值；

（3）将表格中的数据看作五个点的坐标，则从这五个点中随机抽取3个点，记落在直线右下方的点的个数为，求的分布列以及期望.

参考公式： ， .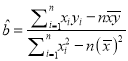

Answer 1

【答案】（1）散点图见解析

（2）回归直线方程为，故当时，

（3）分布列见解析；

【解析】试题分析：

(1)由题中所给的数据绘制散点图即可；

(2)由题意可得， ，则线性回归方程为，当时， .

(3) 的可能取值为1,2,3，利用超几何分布可得分布列，然后计算数学期望为.

试题解析：

（1）散点图如图所示：

（2）依题意， ， ，

， ，

，∴；

∴回归直线方程为，故当时， .

（3）可以判断，落在直线右下方的点满足，

故符合条件的点的坐标为，故的可能取值为1,2,3；

， ， ，

故的分布列为

故.