题目内容
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 过点
过点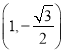 ,记椭圆
,记椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的点,直线
的点,直线![]() 与直线
与直线![]() 分别交于点
分别交于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() ,记
,记![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
【答案】(1)椭圆![]() 的方程为
的方程为![]() (2)
(2)![]()
【解析】试题分析:
(1)由题意求得![]() ,
, ![]() ,
, ![]() ,故椭圆
,故椭圆![]() 的方程为
的方程为![]() .
.
(2)很明显直线的斜率存在,设出切线方程,联立直线与椭圆的方程,结合韦达定理得到关于实数![]() 的不等式组,结合不等式组的性质和题意讨论可得
的不等式组,结合不等式组的性质和题意讨论可得![]() .
.
试题解析:
(1)依题意, 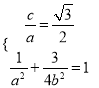 ,解得
,解得![]() ,
, ![]() ,
, ![]() ,
,
故椭圆![]() 的方程为
的方程为![]() .
.
(2)依题意, ![]() ,
, ![]() ,直线
,直线![]() ,
,
设![]() ,则
,则![]() .
.
直线![]() 的方程为
的方程为![]() ,令
,令![]() ,得点
,得点![]() 的纵坐标为
的纵坐标为![]() ;
;
直线![]() 的方程为
的方程为![]() ,令
,令![]() ,得点
,得点![]() 的纵坐标为
的纵坐标为![]() ;
;
由题知,椭圆在点![]() 处切线斜率存在,可设切线方程为
处切线斜率存在,可设切线方程为![]() ,
,
由![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ,
,
整理得: ![]() ,
,
将![]() ,
, ![]() 代入上式并整理得
代入上式并整理得![]() ,解得
,解得![]() ,
,
所以点![]() 处的切线方程为
处的切线方程为![]() .
.
令![]() 得,点
得,点![]() 的纵坐标为
的纵坐标为![]() ,
,
设![]() ,所以
,所以![]() ,
,
所以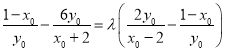 ,
,
所以 ,
,
将![]() 代入上式,
代入上式, ![]() ,因为
,因为![]() ,所以
,所以![]() .
.

练习册系列答案
相关题目
【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,
(单位:元),继续购买该险种的投保人称为续保人,
续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
随机调查了该险种的400名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 |
|
频数 | 120 | 100 | 60 | 60 | 40 | 20 |
(Ⅰ)记A为事件:“一续保人本年度的保费不高于基本保费”.求![]() 的估计值;
的估计值;
(Ⅱ)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的190%”.
求![]() 的估计值;
的估计值;
(III)求续保人本年度的平均保费估计值.