题目内容
在数列{an}中,a1=1,an+1= 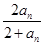 (n∈N*).
(n∈N*).
(Ⅰ)求a2, a3, a4;
(Ⅱ)猜想an,并用数学归纳法证明;
(Ⅲ)若数列bn= 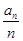 ,求数列{bn}的前n项和sn。
,求数列{bn}的前n项和sn。
(Ⅰ)∴a2= 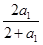 =
=  ,a3 =
,a3 = 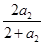 =
= 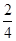 ,a4 =
,a4 =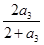 =
=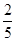 .(Ⅱ)略
.(Ⅱ)略
(Ⅲ)sn=b1+b2+…+bn=2[(1- )+(
)+( -
-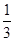 )+…+(
)+…+(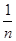 -
-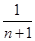 )]=2[1-
)]=2[1-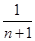 ]=
]=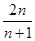
解析

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
等比数列 中,
中, ,
, ,
, 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且 ,
, ,
, 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
| | 第一列 | 第二列 | 第三列 |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 6 | 4 | 14 |
| 第三行 | 9 | 8 | 18 |
 的通项公式;
的通项公式;(Ⅱ)若数列
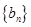 满足:
满足: ,求数列
,求数列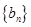 的前
的前 项和
项和 .
. 已知数列 的通项是
的通项是 ,则数列
,则数列 中的正整数项有( )项.
中的正整数项有( )项.
| A.1 | B.2 | C.3 | D.4 |
已知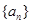 中
中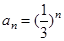 ,把数列
,把数列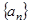 的各项排列成如下的三角形状,
的各项排列成如下的三角形状,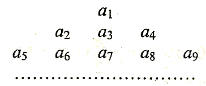
记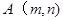 表示第
表示第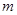 行的第
行的第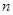 个数,则
个数,则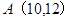 =( )
=( )
A.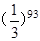 |
B.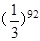 |
C.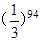 |
D. |
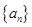 首项
首项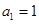 ,公差为
,公差为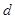 ,且数列
,且数列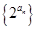 是公比为4的等比数列,
是公比为4的等比数列,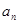 及前
及前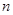 项和
项和 ;
; 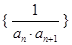 的前
的前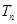 .
.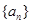 是等差数列,
是等差数列,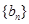 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且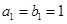 ,
,  ,
,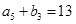
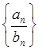 的前n项和
的前n项和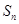 .
.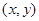 是区域
是区域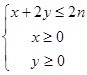 ,(
,(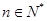 )内的点,目标函数
)内的点,目标函数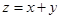 ,
, 的最大值记作
的最大值记作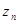 .若数列
.若数列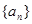 的前
的前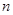 项和为
项和为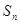 ,
,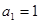 ,且点(
,且点(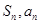 )在直线
)在直线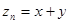 上.
上. 为等比数列;
为等比数列;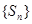 的前
的前 .
.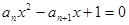 ,
,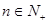 有两根
有两根 和
和 ,且满足
,且满足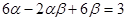 ,
, 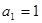
 表示
表示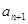 ; (2)证明
; (2)证明 是等比数列;
是等比数列; ,
,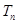 为
为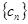 的前n项和,证明
的前n项和,证明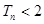 ,(
,(