题目内容
(本小题满分12分)
已知点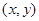 是区域
是区域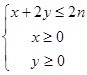 ,(
,(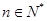 )内的点,目标函数
)内的点,目标函数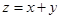 ,
, 的最大值记作
的最大值记作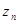 .若数列
.若数列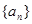 的前
的前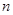 项和为
项和为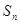 ,
,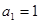 ,且点(
,且点(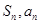 )在直线
)在直线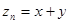 上.
上.
(Ⅰ)证明:数列 为等比数列;
为等比数列;
(Ⅱ)求数列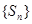 的前
的前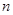 项和
项和 .
.
解:(Ⅰ)见解析;
(Ⅱ)∴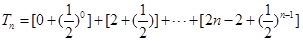
解析试题分析:(1)根据当直线过点 时,目标函数取得最大值,故
时,目标函数取得最大值,故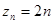
进而得到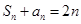 的关系式,然后利用通项公式与前n项和的关系得到证明。
的关系式,然后利用通项公式与前n项和的关系得到证明。
(2)由(Ⅰ)得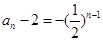 ,∴
,∴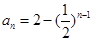 ,根据通项公式的特点,分组求和得到结论。
,根据通项公式的特点,分组求和得到结论。
解:(Ⅰ)由已知当直线过点 时,目标函数取得最大值,故
时,目标函数取得最大值,故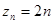
∴方程为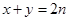
∵(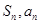 )在直线
)在直线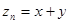 上,
上,
∴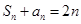 ①
①
∴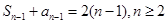 ②
②
由①-②得,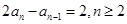 ∴
∴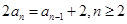 ,
,
∴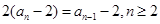
∵ , ∴数列
, ∴数列 以
以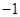 为首项,
为首项,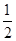 为公比的等比数列
为公比的等比数列
(Ⅱ)由(Ⅰ)得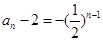 ,∴
,∴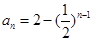
∵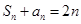 , ∴
, ∴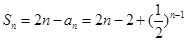
∴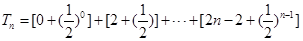
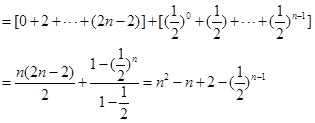
考点:本试题主要考查了等比数列的定义和数列的求和的综合运用。
点评:解决该试题的关键是分析出线性目标函数的最优解,然后得到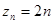 ,然后得到
,然后得到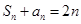 。
。

练习册系列答案
相关题目
数列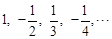 的一个通项公式为( )
的一个通项公式为( )
A.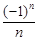 | B.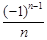 | C.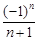 | D.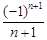 |
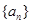 的前n项和为
的前n项和为 ,已知
,已知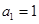 ,
,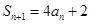
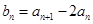 ,证明数列
,证明数列 是等比数列 (2)求数列
是等比数列 (2)求数列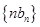 的前
的前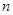 项和
项和
 的各项均为正数,且满足
的各项均为正数,且满足 ,
,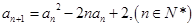 .
. 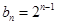 ,令
,令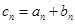 ,求数列
,求数列 的前
的前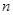 项和
项和
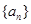 中,
中,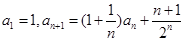 ,
, 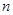 项和
项和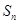
 的各项均为正数,
的各项均为正数,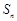 为其前
为其前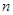 项和,对于任意
项和,对于任意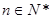 ,总有
,总有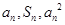 成等差数列.
成等差数列. ,数列
,数列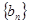 的前
的前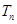 ,求证:
,求证: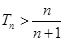 .
.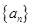 中,
中,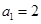 ,
,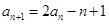 (
(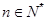 ),数列
),数列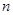 项和为
项和为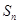 。(1)证明:数列
。(1)证明:数列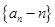 是等比数列,并求数列
是等比数列,并求数列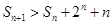 。
。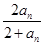 (n∈N*).
(n∈N*).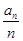 ,求数列{bn}的前n项和sn。
,求数列{bn}的前n项和sn。