题目内容
(本小题13分)已知抛物线的顶点在坐标原点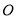 ,焦点
,焦点 在
在 轴上,抛物线上的点
轴上,抛物线上的点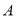 到
到 的距离为2,且
的距离为2,且 的横坐标为1.直线
的横坐标为1.直线 与抛物线交于
与抛物线交于 ,
, 两点.
两点.
(1)求抛物线的方程;
(2)当直线 ,
,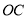 的倾斜角之和为
的倾斜角之和为 时,证明直线
时,证明直线 过定点.
过定点.
(1)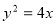 ,(2)
,(2)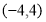
【解析】
试题分析:首先根据抛物线的焦半径公式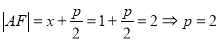 ,得抛物线方程
,得抛物线方程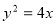 ,第二步设而不求思想,联立方程组
,第二步设而不求思想,联立方程组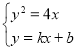 得
得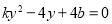 ,借助
,借助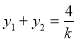 ,
,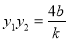 ,直设线
,直设线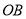 ,
,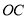 的倾斜角分别为
的倾斜角分别为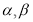 ,斜率分别为
,斜率分别为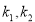 ,则
,则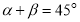 ,有
,有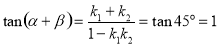 ,因
,因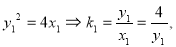 同理
同理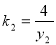 代入上式得:
代入上式得:
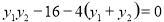 ,再把
,再把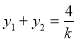 ,
,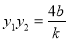 代入得:
代入得: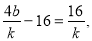 即
即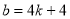 ,
,
写出直线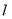 的方程为
的方程为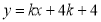 ,整理得
,整理得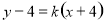 ,所以直线
,所以直线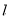 过定点
过定点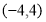
试题解析:(1)设抛物线方程为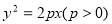 ,由抛物线的定义知
,由抛物线的定义知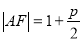 ,又
,又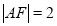 所以
所以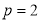 ,所以抛物线的方程为
,所以抛物线的方程为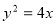 .
.
(2)设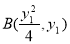 ,
,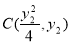 联立
联立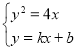 ,整理得
,整理得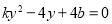 (依题意
(依题意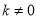 )
)
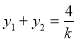 ,
,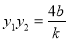 ,
,
设直线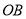 ,
,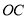 的倾斜角分别为
的倾斜角分别为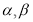 ,斜率分别为
,斜率分别为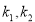 ,则
,则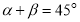
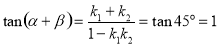 其中
其中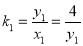 ,
,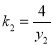 ,代入上式整理得:
,代入上式整理得:
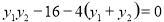 ,把
,把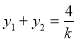 ,
,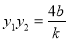 代入得:,
代入得:,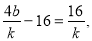 即
即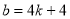
则直线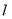 的方程为
的方程为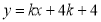 ,整理得
,整理得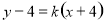 ,所以直线
,所以直线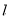 过定点
过定点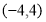
考点:1.焦半径公式;2.联立方程组,设而不求;3.根与系数关系;4.巧设抛物线上的点;5.巧用斜率;6.直线过定点;

练习册系列答案
相关题目


 ,且
,且 ,则M的值是
,则M的值是 C.
C. D.400
D.400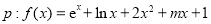 在
在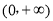 内单调递增,
内单调递增,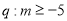 ,则
,则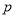 是
是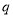 的( )
的( ) 为非零实数,且
为非零实数,且 ,则下列命题成立的是 ( )
,则下列命题成立的是 ( ) B.
B. C.
C. D.
D.
 a2.
a2.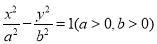 的右焦点为F,若过点F且倾斜角为
的右焦点为F,若过点F且倾斜角为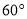 的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )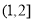 B.
B. C.
C.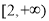 D.
D.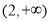
 满足
满足 ,且
,且 的导数
的导数 ,则不等式
,则不等式 .
.