题目内容

9．已知F1，F2是椭圆$\frac{x^2}{25}+\frac{y^2}{9}$=1的两个焦点，过F1作直线与椭圆相交于M，N两点，则△MNF2的周长为20．

分析 由椭圆$\frac{x^2}{25}+\frac{y^2}{9}$=1求得a=5，由椭圆的定义可知：|F1M|+|F2M|=2a=10，|F1N|+|F2N|=2a=10，则△MNF2的周长4a=20．

解答 解：椭圆$\frac{x^2}{25}+\frac{y^2}{9}$=1焦点在x轴上，a=5，b=3，c=4，
利用椭圆的定义可知：|F1M|+|F2M|=2a=10，|F1N|+|F2N|=2a=10，
∴△MNF2的周长为|F1M|+|F2M|+F1N|+|F2N|=4a=20，
故答案为：20．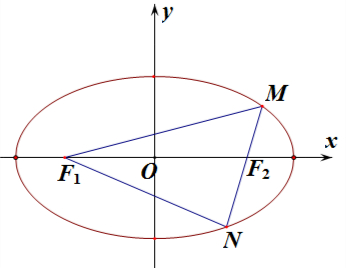

点评 本题主要考查了椭圆的简单性质．考查椭圆的第一定义的应用，考查焦点三角形的周长，属于基础题．

练习册系列答案
相关题目
19．已知f（x）是定义在R上的偶函数，且满足xf′（x）＜0（x≠0），设a=f$（{log_{\frac{1}{4}}}7）$，b=f（log23），c=f（0.2-0.6），则a，b，c的大小关系是（　　）
A．c＜a＜bB．c＜b＜aC．b＜c＜aD．a＜b＜c
20．函数f（x）=$\left\{\begin{array}{l}{|lnx-1|，x＞0}\\{-{x}^{2}-2x+2，x≤0}\end{array}\right.$，若f（a）=f（b）=f（c）=f（d）且a＜b＜c＜d，给出下列三个结论：
①abcd∈（0，e2]；
②a+b+c+d∈（e3+$\frac{1}{e}$-2，e4+$\frac{1}{{e}^{2}}$-2]；
③已知关于x的方程f（x）+（-1）kx-t=0恰有三个不同实根，若k为偶数，则t∈[2，$\frac{9}{4}$]；若k为奇数，则t=[2，$\frac{17}{4}$]；其中正确的结论有（　　）个．
A．0B．1C．2D．3
17．定义在R上的函数y=f（x）满足f（x）•f（x+5）=3，f（1）=2，则f（2016）=$\frac{3}{2}$．
4．如图是某几何体的三视图，则该几何体的表面积为63．
14．已知函数f（x）=x3-3x+5，当x∈[-2，2]时，f（x）＜m恒成立，则实数m的取值范围为m＞7．．
1．已知函数f（x）=$\frac{1}{2}{x^2}$-alnx（a∈R）．
（1）若函数f（x）在（0，+∞）为增函数，求实数a的取值范围；
（2）讨论方程f（x）=0解的个数，并说明理由．
18．有下面四个判断：①命题“设a、b∈R，若a+b≠6，则a≠3或b≠3”是一个假命题；②若“p或q”为真命题，则p、q均为真命题；③在△ABC中，“A＞30o”是“sinA＞$\frac{1}{2}$”的充分不必要条件；④设向量$\overrightarrow{a}$=（sin2θ，cosθ），$\overrightarrow{b}$=（cosθ，1），则“$\overrightarrow{a}$∥$\overrightarrow{b}$”是“tanθ=$\frac{1}{2}$”成立的必要不充分条件．其中所有错误的判断有①②③．（填序号）
19．已知函数f（x）=2sinωx，其中常数ω＞0．
（Ⅰ）令ω=1，求函数$F（x）=f（x）+{[f（x+\frac{π}{2}）]}^{2}$在$[-\frac{π}{2}，0]$上的最大值；
（Ⅱ）若函数$g（x）=2-f（x）+2\sqrt{3}cosωx$的周期为π，求函数g（x）的单调递增区间，并直接写出g（x）在$[\frac{3π}{4}，\frac{23π}{4}]$的零点个数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网