题目内容
1.在数列{an}中,${a_1}=1,{a_{n+1}}=2{a_n}+1\;(n∈{N^+})$.(Ⅰ)证明数列{an+1}成等比数列,并求{an}的通项公式;
(Ⅱ)令bn=(2n+1)(an+1),求数列{bn}的前n项和Sn.
分析 (Ⅰ)通过对an+1=2an+1变形可知an+1+1=2(an+1),进而可知数列{an+1}是首项、公比均为1的等比数列,计算即得结论;
(Ⅱ)通过(I)可知bn=(2n+1)•2n,利用错位相减法计算即得结论.
解答 (Ⅰ)证明:∵an+1=2an+1,
∴an+1+1=2(an+1),
又∵a1+1=1+1=2,
∴数列{an+1}是首项、公比均为1的等比数列,
∴an+1=2n,an=-1+2n;
(Ⅱ)解:由(I)可知bn=(2n+1)(an+1)=(2n+1)•2n,
则Sn=3•21+5•22+…+(2n+1)•2n,
2Sn=3•22+5•23+…+(2n+1)•2n+1,
两式相减得:-Sn=3•21+2(22+23+…+2n)-(2n+1)•2n+1
=3•21+2•$\frac{4(1-{2}^{n-1})}{1-2}$-(2n+1)•2n+1
=-2-(2n-1)•2n+1,
∴Sn=2+(2n-1)•2n+1.
点评 本题考查数列的通项及前n项和,考查错位相减法,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
12.三棱锥P-ABC的三条侧棱两两垂直,三个侧面的面积分别是$\frac{\sqrt{2}}{2}$、$\frac{\sqrt{3}}{2}$、$\frac{\sqrt{6}}{2}$,则该三棱锥的外接球的体积是( )
| A. | $\frac{\sqrt{2}}{3}$π | B. | $\frac{8\sqrt{2}}{3}$π | C. | $\sqrt{6}$π | D. | 8$\sqrt{6}$π |
9.定义在R上的函数f(x)满足$f({x+2})=\frac{1}{2}f(x)$,当x∈[0,2)时,$f(x)=\left\{\begin{array}{l}\frac{1}{2}-2{x^2},0≤x<1\\-{2^{1-|{x-\frac{3}{2}}|}},1≤x<2\end{array}\right.$,函数g(x)=x3+3x2+m.若?s∈[-4,-2),?t∈[-4,-2),不等式f(s)-g(t)≥0成立,则实数m的取值范围是( )
| A. | (-∞,-12] | B. | (-∞,-4] | C. | (-∞,8] | D. | $({-∞,\frac{31}{2}}]$ |
13.若f(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$,g(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$则下列等式不正确的是( )
| A. | f(2x)=2g2(x)+1 | B. | f2(x)-g2(x)=1 | C. | f2(x)+g2(x)=f(2x) | D. | f(x+y)=f(x)f(y)-g(x)g(y) |
11.在△ABC中,角A、B、C的对边分别为a、b、c,若cos2A+cos2C+$\sqrt{2}$sinAsinC=1+cos2B.则$\sqrt{2}$sinA+cosC的最大值是( )
| A. | 1 | B. | 2 | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\sqrt{5}$ |
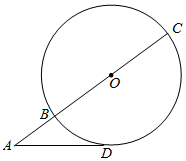 如图,BC为⊙O的直径,且BC=6,延长CB与⊙O在点D处的切线交于点A,若AD=4,则AB=2.
如图,BC为⊙O的直径,且BC=6,延长CB与⊙O在点D处的切线交于点A,若AD=4,则AB=2.