题目内容
已知函数 ,
,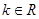 .
.
(1)若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)若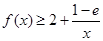 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)设 ,若对任意的两个实数
,若对任意的两个实数 满足
满足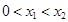 ,总存在
,总存在 ,使得
,使得
 成立,证明:
成立,证明: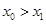 .
.
(1) 函数 的单调递减区间为(0,1),单调递增区间为(1,
的单调递减区间为(0,1),单调递增区间为(1,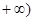 ;(2) 实数
;(2) 实数 的取值范围
的取值范围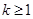 ;(3) 详见解析.
;(3) 详见解析.
解析试题分析:(1)若 ,求函数
,求函数 的单调区间,由于含有对数式,可求出
的单调区间,由于含有对数式,可求出 导数
导数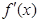 ,在定义域内解不等式
,在定义域内解不等式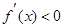 ,
,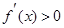 即得函数单调区间;(2)
即得函数单调区间;(2)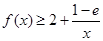 恒成立,这是恒成立求参数范围,常采用分离常数法,故本题分离出参数
恒成立,这是恒成立求参数范围,常采用分离常数法,故本题分离出参数 后变为
后变为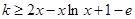 恒成立,构造函数
恒成立,构造函数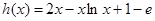 ,则问题转化为
,则问题转化为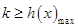 ,利用导数可求得
,利用导数可求得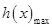 ,从而得实数
,从而得实数 的取值范围;(3)证明:
的取值范围;(3)证明: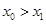 ,由已知
,由已知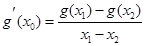 ,可得
,可得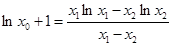 ,进而可变形为
,进而可变形为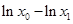
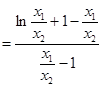 ,只需证明
,只需证明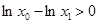 ,设
,设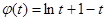 ,其中
,其中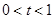 ,用导数可判断
,用导数可判断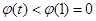 ,又
,又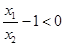 ,可得结论.
,可得结论.
试题解析:(1)当 时,函数
时,函数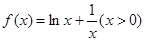 ,
,
则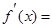
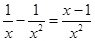 .
.
当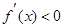 时,
时,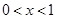 ,当
,当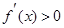 时,
时,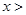 1,
1,
则函数 的单调递减区间为(0,1),单调递增区间为(1,
的单调递减区间为(0,1),单调递增区间为(1,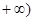 . 4分
. 4分
(2)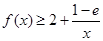 恒成立,即
恒成立,即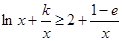 恒成立,整理得
恒成立,整理得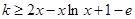 恒成立.
恒成立.
设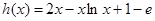 ,则
,则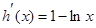 ,令
,令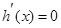 ,得
,得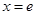 .当
.当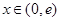 时,
时,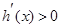 ,函数
,函数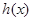 单调递增,当
单调递增,当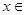
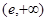 时,
时,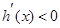 ,函数
,函数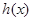 单调递减,因此当
单调递减,因此当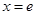 时,
时,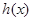 取得最大值1,因而
取得最大值1,因而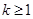 . 8分
. 8分
(3)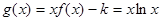 ,
,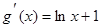 .
.
因为对任意的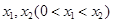 总存在
总存在 ,使得
,使得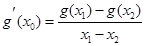 成立,
成立,
所以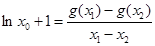 , 即
, 即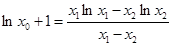 ,
,
即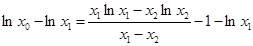
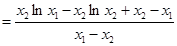
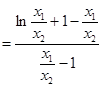 . 12分
. 12分
设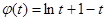 ,其中
,其中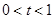 ,则
,则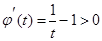 ,因而
,因而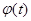 在区间(0,1)上单调递增,
在区间(0,1)上单调递增,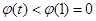 ,又
,又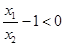 .
.
所以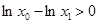 ,即
,即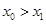 . 14分
. 14分
考点:导数在最大值、最小值问题中的应用;利用导数研究函数的单调性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
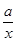 +xln x,g(x)=x3-x2-3.
+xln x,g(x)=x3-x2-3.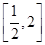 ,都有f(s)≥g(t)成立,求实数a的取值范围.
,都有f(s)≥g(t)成立,求实数a的取值范围.
 存在极大值和极小值,求
存在极大值和极小值,求 的取值范围;
的取值范围; 分别为
分别为 的极大值和极小值,其中
的极大值和极小值,其中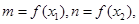 且
且 求
求 的取值范围.
的取值范围.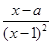 ,x∈(1,+∞).
,x∈(1,+∞). 其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.
其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.
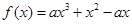 ,其中
,其中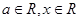 .
. 时,求函数
时,求函数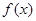 在
在 处的切线方程;
处的切线方程; 的取值范围;
的取值范围;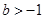 ,如果存在
,如果存在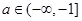 ,使得函数
,使得函数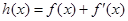
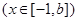 在
在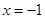 处取得最小值,试求
处取得最小值,试求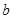 的最大值.
的最大值. ,
, ,
, ,其中
,其中 ,且
,且 .
. 时,求函数
时,求函数 的最大值;
的最大值; 的单调区间;
的单调区间; 若对任意给定的非零实数
若对任意给定的非零实数 ,存在非零实数
,存在非零实数 (
( ),使得
),使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.