题目内容
已知函数
(1)若函数 存在极大值和极小值,求
存在极大值和极小值,求 的取值范围;
的取值范围;
(2)设 分别为
分别为 的极大值和极小值,其中
的极大值和极小值,其中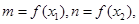 且
且 求
求 的取值范围.
的取值范围.
(1)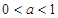 ;(2)
;(2)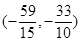
解析试题分析:(1)因为函数 ,所以要求函数
,所以要求函数 存在极大值和极小值即对函数的求导,要保证导函数的对应的方程有两个不相等的正实根.所以通过判别式大于零和韦达定理中根与系数的关系即可得到结论.
存在极大值和极小值即对函数的求导,要保证导函数的对应的方程有两个不相等的正实根.所以通过判别式大于零和韦达定理中根与系数的关系即可得到结论.
(2)根据极大值与极小值的含义得到两个相应的方程,又由两个极值点的关系,将其中一个消去,由两个极值相加可得关于关于极大值点的等式从而通过基本不等式求最值即可.
试题解析:(1)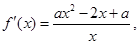 其中
其中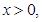
由题设知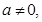 且关于
且关于 的方程
的方程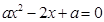 有两个不相等的正数根,
有两个不相等的正数根,
记为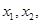 满足
满足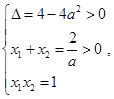 化简得
化简得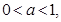
经检验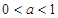 满足题设,故为所求.
满足题设,故为所求.
(2)方法一:由题设结合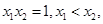 知
知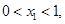
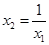 ,
,
且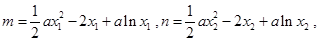
所以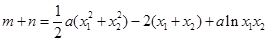
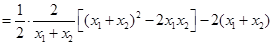
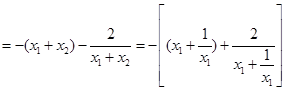 ,
,
因为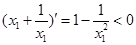 ,所以
,所以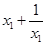 在区间
在区间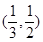 是减函数,
是减函数,
所以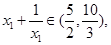 设
设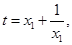 且
且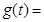
 ,
,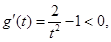
所以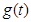 在区间
在区间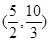 上是减函数,
上是减函数,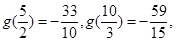 所以
所以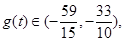
因此
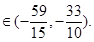
方法二:由题设结合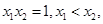 知
知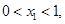
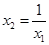
且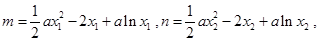
所以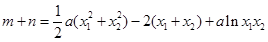
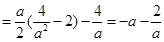 ,
,
设 ,
,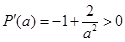 ,
,
所以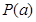 在区间
在区间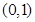 上是增函数,
上是增函数,
而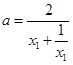 ,设
,设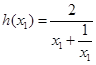 ,则
,则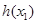 在
在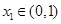 时是增函数,
时是增函数,
所以当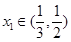 时,
时,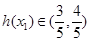 ,即
,即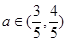 ,
,
所以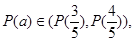 且
且
因此
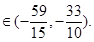
方法三:由方法一知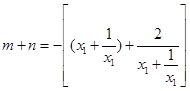
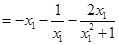
设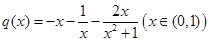 ,则
,则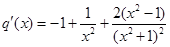
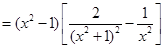
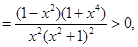
所以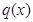 在区间
在区间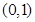 上是增函数,而
上是增函数,而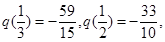
所以
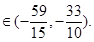
方法四:前同方法二知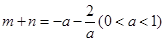 ,
,
当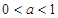 时,关于
时,关于 的方程
的方程 有两个不相等的正数根
有两个不相等的正数根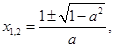
那么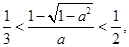 即
即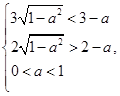 解得
解得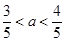 ,
,
下同方法二.
考点:1.利用导数求极值.2.利用基本不等式求极值.3.函数与不等式的关系.4.消元解方程的思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 x3+
x3+ ax2+bx.
ax2+bx. 若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围. 的导函数为
的导函数为 ,
, 的图象在点
的图象在点 ,
, 处的切线方程为
处的切线方程为 ,且
,且 ,直线
,直线 是函数
是函数 的图象的一条切线.
的图象的一条切线. 的值;
的值; 对于任意
对于任意 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,
,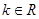 .
. ,求函数
,求函数 的单调区间;
的单调区间;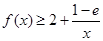 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,若对任意的两个实数
,若对任意的两个实数 满足
满足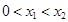 ,总存在
,总存在 ,使得
,使得
 成立,证明:
成立,证明: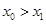 .
. (f′(x)是f(x)的导函数)在区间(t,3)上总不是单调函数,求m的取值范围;
(f′(x)是f(x)的导函数)在区间(t,3)上总不是单调函数,求m的取值范围; ×…×
×…× <
< (n≥2,n∈N*)
(n≥2,n∈N*) .
. .的单调区间;
.的单调区间; 的极值.
的极值. .
. ,求
,求 在点
在点 处的切线方程;
处的切线方程;