题目内容
已知在平面直角坐标系中,圆C:(x-a)2+(y-b)2=10(a>b>0)在直线x+2y=0上截得的弦长为2
(1)求a,b满足的关系;
(2)当a2+b2取得最小值时,求圆C的方程.
| 5 |
(1)求a,b满足的关系;
(2)当a2+b2取得最小值时,求圆C的方程.
考点:直线与圆相交的性质
专题:计算题,直线与圆
分析:(1)求出圆心到直线的距离,利用圆C:(x-a)2+(y-b)2=10(a>b>0)在直线x+2y=0上截得的弦长为2
,即可求a,b满足的关系;
(2)利用配方法,确定a2+b2最小值,即可求圆C的方程.
| 5 |
(2)利用配方法,确定a2+b2最小值,即可求圆C的方程.
解答:
解:(1)圆心到直线的距离为
∵圆C:(x-a)2+(y-b)2=10(a>b>0)在直线x+2y=0上截得的弦长为2
,
∴2
=2
,
∵a>b>0,
∴a+2b=5;
(2)a2+b2=(5-2b)2+b2=5b2-20b+25=5(b-2)2+5,
∴b=2时,a2+b2取得最小值5,此时a=1,
∴圆C的方程为:(x-1)2+(y-2)2=10.
| |a+2b| | ||
|
∵圆C:(x-a)2+(y-b)2=10(a>b>0)在直线x+2y=0上截得的弦长为2
| 5 |
∴2
| 5 |
10-
|
∵a>b>0,
∴a+2b=5;
(2)a2+b2=(5-2b)2+b2=5b2-20b+25=5(b-2)2+5,
∴b=2时,a2+b2取得最小值5,此时a=1,
∴圆C的方程为:(x-1)2+(y-2)2=10.
点评:本题考查圆的方程,考查直线与圆的位置关系,考查配方法的运用,属于中档题.

练习册系列答案
相关题目
已知f(tanx)=sin2x,则f(-1)的值是( )
| A、1 | ||
| B、-1 | ||
C、
| ||
| D、0 |
已知
(sin x+a)dx=1,则常数a的值为( )
| ∫ |
0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
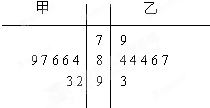 如图是校园“十佳歌手”大奖赛上,七位评委为甲、乙两位选手打出的分数的茎叶图.
如图是校园“十佳歌手”大奖赛上,七位评委为甲、乙两位选手打出的分数的茎叶图.