题目内容
18.已知数列{an}满足:对任意的n∈N*均有an+1=kan+3k-3,其中k为不等于0与1的常数,若ai∈{-678,-78,-3,22,222,2222},i=2,3,4,5,则满足条件的a1所有可能值的和为$\frac{6023}{3}$.分析 依题意,可得an+1+3=k(an+3),再对a1=-3与a1≠-3讨论,特别是a1≠-3时对公比k分|k|>1与|k|<1,即可求得a1所有可能值,从而可得答案.
解答 解:∵an+1=kan+3k-3,
∴an+1+3=k(an+3),
∴①若a1=-3,则a1+1+3=k(a1+3)=0,a2=-3,同理可得,a3=a4=a5=-3,即a1=-3复合题意;
②若a1≠-3,k为不等于0与1的常数,则数列{an+3}是以k为公比的等比数列,
∵ai∈{-678,-78,-3,22,222,2222},i=2,3,4,5,
an+3可以取-675,-75,25,225,
∵-75=25×(-3),225=-75×(-3),-675=225×(-3),
∴若公比|k|>1,则k=-3,由a2+3=22+3=-3(a1+3)得:a1=-$\frac{25}{3}$-3=-$\frac{34}{3}$;
若公比|k|<1,则k=-$\frac{1}{3}$,由a2+3=-675=-$\frac{1}{3}$(a1+3)得:a1=2025-3=2022;
综上所述,满足条件的a1所有可能值为-3,-$\frac{34}{3}$,2022.
∴a1所有可能值的和为:-3-$\frac{34}{3}$+2022=$\frac{6023}{3}$..
故答案为:$\frac{6023}{3}$.
点评 本题考查数列递推式的应用,考查等价转化思想与分类讨论思想的综合运用,对an+1+3=k(an+3)的理解与应用是难点,对公比k分|k|>1与|k|<1讨论是关键,考查逻辑思维与推理运算能力,属于难题.

练习册系列答案
相关题目
7.已知0<a<1,logax<logay<0,则( )
| A. | 1<y<x | B. | 1<x<y | C. | x<y<1 | D. | y<x<1 |
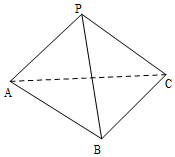 在正三棱锥P-ABC中,已知底面等边三角形的边长为6,侧棱长为4.
在正三棱锥P-ABC中,已知底面等边三角形的边长为6,侧棱长为4. 如图,已知曲线${C_1}:y=\frac{2x}{x+1}\;\;(x>0)$及曲线${C_2}:y=\frac{1}{3x}\;\;(x>0)$,C1上的点P1的横坐标为${a_1}\;(0<{a_1}<\frac{1}{2})$.从C1上的点${P_n}\;(n∈{N^*})$作直线平行于x轴,交曲线C2于Qn点,再从C2上的点${Q_n}\;(n∈{N^*})$作直线平行于y轴,交曲线C1于Pn+1点,点Pn(n=1,2,3…)的横坐标构成数列{an}.
如图,已知曲线${C_1}:y=\frac{2x}{x+1}\;\;(x>0)$及曲线${C_2}:y=\frac{1}{3x}\;\;(x>0)$,C1上的点P1的横坐标为${a_1}\;(0<{a_1}<\frac{1}{2})$.从C1上的点${P_n}\;(n∈{N^*})$作直线平行于x轴,交曲线C2于Qn点,再从C2上的点${Q_n}\;(n∈{N^*})$作直线平行于y轴,交曲线C1于Pn+1点,点Pn(n=1,2,3…)的横坐标构成数列{an}.