题目内容
7. 如图所示,在四边形ABCD中,D=2B,且$AD=2,CD=6,cosB=\frac{{\sqrt{3}}}{3}$.
如图所示,在四边形ABCD中,D=2B,且$AD=2,CD=6,cosB=\frac{{\sqrt{3}}}{3}$.(1)求△ACD的面积;
(2)若$BC=4\sqrt{3}$,求AB的长.
分析 (1)利用已知条件求出D角的正弦函数值,然后求△ACD的面积;
(2)利用余弦定理求出AC,通过BC=4$\sqrt{3}$,利用余弦定理求解AB的长.
解答 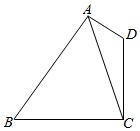 解:(1)∵$cosB=\frac{{\sqrt{3}}}{3},0<B<π,可求:sinB=\frac{{\sqrt{6}}}{3}$.
解:(1)∵$cosB=\frac{{\sqrt{3}}}{3},0<B<π,可求:sinB=\frac{{\sqrt{6}}}{3}$.
∴$sinD=sin2B=2sinBcosB=\frac{{2\sqrt{2}}}{3}$.
∴${S_{△ACD}}=\frac{1}{2}•AD•CD•sinD=4\sqrt{2}$.…(6分)
(2)∵AD=2,CD=6,cosD=2cos2B-1=-$\frac{1}{3}$,
∴在△ACD中,由余弦定理知,$AC=\sqrt{A{D^2}+C{D^2}-2AD•CD•cosD}$=$\sqrt{4+36-2×2×6×(-\frac{1}{3})}$=4$\sqrt{3}$,
∵在△ABC中,$cosB=\frac{{A{B^2}+B{C^2}-A{C^2}}}{2AB•BC}=\frac{{\sqrt{3}}}{3}$,
∴解得:AB=8.…(12分)
点评 本题考查余弦定理以及正弦定理的应用,基本知识的考查,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
17.设F1,F2是双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的两个焦点,点P在双曲线上,且∠F1PF2=60°,则|PF1||PF2|的值为( )
| A. | 36 | B. | 16$\sqrt{3}$ | C. | 16 | D. | 64 |
15.在△ABC中,角A,B,C的对边分别是a,b,c,且满(2a-c)cosB=bcosC,则A的取值范围( )
| A. | (0,$\frac{2π}{3}$) | B. | (0,π) | C. | ($\frac{π}{3}$,$\frac{2π}{3}$) | D. | ($\frac{2π}{3}$π) |
12.在△ABC中,若b=8,c=3,A=60°,则此三角形外接圆的半径为( )
| A. | $\frac{{8\sqrt{2}}}{3}$ | B. | $\frac{14}{3}\sqrt{3}$ | C. | $\frac{7}{3}$ | D. | $\frac{{7\sqrt{3}}}{3}$ |
19.若复数z满足($\sqrt{3}$+i)z=4i(i为虚数单位),则复数z的共轭复数为( )
| A. | $\sqrt{3}$+i | B. | $\sqrt{3}$-i | C. | 1+$\sqrt{3}$i | D. | 1-$\sqrt{3}$i |