题目内容
已知正方形的面积是5cm2，图阴影部分是两个四分之一圆所围成的面积，求阴影部分的面积．考点：定积分
专题：导数的概念及应用
分析：先建系，构造曲线方程和直线方程，阴影部分的面积转化为=2
[
-（-x+
）]dx，再根据定积分的几何意义即可求出．
| ∫ |
0 |
| 5-x2 |
| 5 |
解答：
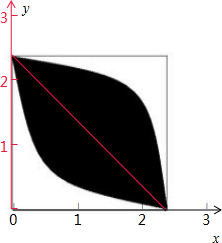解：方法一：如图，以正方形的边长为x轴和y轴，
则圆的直线方程为x2+y2=5，
则曲线的方程为y=
，0≤x≤
，
直线方程为y=-x+
，
所以阴影部分的面积为S=2
[
-（-x+
）]dx，
因为
dx表示是圆的面积的四分之一，故
dx=
×π×5，
（-x+
）dx表示三角形的面积，即为正方形面积的一半，故
（-x+
）dx=
，
故S=2
[
-（-x+
）]dx=2（
-
）=
-5，
所以阴影部分的面积为
-5．
方法二，阴影部分的面积等于半圆的面积减去正方形的面积，故S=
π×5-5=
-5．
解：方法一：如图，以正方形的边长为x轴和y轴，则圆的直线方程为x2+y2=5，
则曲线的方程为y=
| 5-x2 |
| 5 |
直线方程为y=-x+
| 5 |
所以阴影部分的面积为S=2
| ∫ |
0 |
| 5-x2 |
| 5 |
因为
| ∫ |
0 |
| 5-x2 |
| ∫ |
0 |
| 5-x2 |
| 1 |
| 4 |
| ∫ |
0 |
| 5 |
| ∫ |
0 |
| 5 |
| 5 |
| 2 |
故S=2
| ∫ |
0 |
| 5-x2 |
| 5 |
| 5π |
| 4 |
| 5 |
| 2 |
| 5π |
| 2 |
所以阴影部分的面积为
| 5π |
| 2 |
方法二，阴影部分的面积等于半圆的面积减去正方形的面积，故S=
| 1 |
| 2 |
| 5π |
| 2 |
点评：本题主要考查了的定积分的几何意义，属于基础题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
