题目内容
7.已知椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1(m>n>0)的离心率为$\frac{1}{2}$,且有一个焦点与抛物线y2=16x的焦点重合,则椭圆的短轴长为8$\sqrt{3}$.分析 利用椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{n}$=1(m>n>0)的离心率为$\frac{1}{2}$,可得$\frac{m-n}{m}$=$\frac{1}{{2}^{2}}$=$\frac{1}{4}$,所以4n=3m,利用焦点与抛物线y2=16x的焦点重合,求出m,n,即可求出椭圆的短轴长.
解答 解:由已知得$\frac{m-n}{m}$=$\frac{1}{{2}^{2}}$=$\frac{1}{4}$,所以4n=3m,
因为抛物线y2=16x的焦点为(4,0),而椭圆的右焦点为(c,0),
所以c=4,得m-n=42=16,解得m=64,n=48,
所以椭圆的短轴长为2$\sqrt{n}$=2$\sqrt{48}$=8$\sqrt{3}$.
故答案为:8$\sqrt{3}$.
点评 本题考查椭圆、抛物线的性质,考查学生的计算能力,确定几何量是关键.

练习册系列答案
相关题目
12.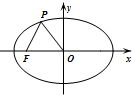 如图,已知椭圆C的中心为原点O,F(-2$\sqrt{5}$,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( )
如图,已知椭圆C的中心为原点O,F(-2$\sqrt{5}$,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( )
 如图,已知椭圆C的中心为原点O,F(-2$\sqrt{5}$,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( )
如图,已知椭圆C的中心为原点O,F(-2$\sqrt{5}$,0)为C的左焦点,P为C上一点,满足|OP|=|OF|且|PF|=4,则椭圆C的方程为( )| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{30}$+$\frac{{y}^{2}}{10}$=1 | C. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{45}$+$\frac{{y}^{2}}{25}$=1 |
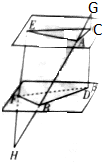 如图,已知α∥β,GH、GD、HE分别交α、β于A、B、C、D、E、F且GA=9,AB=12,BH=16,S△AEC=72,求S△BFD.
如图,已知α∥β,GH、GD、HE分别交α、β于A、B、C、D、E、F且GA=9,AB=12,BH=16,S△AEC=72,求S△BFD.