题目内容
甲、乙、丙三人将参加某项测试，他们能达标的概率分别是0.8，0.6，0.5，求
①三人都达标的概率；
②三人中恰有2人达标的概率．
①三人都达标的概率；
②三人中恰有2人达标的概率．
考点：相互独立事件的概率乘法公式,互斥事件的概率加法公式
专题：概率与统计
分析：①把每个人达标的概率相乘，即得三人都达标的概率．
②分类求出三个人中有2个达标而另一个不达标的概率，相加即得所求．
②分类求出三个人中有2个达标而另一个不达标的概率，相加即得所求．
解答：
解：①三人都达标的概率为0.8×0.6×0.5=0.24．
②三人中恰有2人达标的概率为0.8×0.6（1-0.5）+（1-0.8）×0.6×0.5+0.8×（1-0.4）×0.5
=0.46．
②三人中恰有2人达标的概率为0.8×0.6（1-0.5）+（1-0.8）×0.6×0.5+0.8×（1-0.4）×0.5
=0.46．
点评：本题主要考查相互独立事件的概率乘法公式、互斥事件的概率加法公式的应用，体现了分类讨论的数学思想，属于中档题．
练习册系列答案
相关题目
设非零实数a、b，则“a2+b2≥2ab”是“
+
≥2”成立的（ ）
| a |
| b |
| b |
| a |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
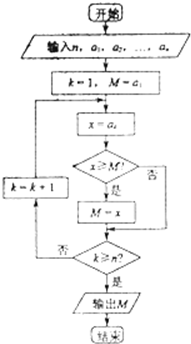
执行如图的程序框图，则输出的M是（ ）
| A、a1，a2，…，an的平均数 |
| B、a1，a2，…，an的中位数 |
| C、a1，a2，…，an中的最大数 |
| D、a1，a2，…，an中的最小数 |
某企业生产一种汽车配件，经抽样统计，该企业生产的配件尺寸的样本频率分布直方图如下．配件尺寸在[60，62）内的为一等品，尺寸在[58，60）或[62，64）内的为二等品，其余为三等品．用频率近似表示概率．