题目内容
19.下列命题错误的是( )| A. | “若x≠a且x≠b,则x2-(a+b)x+ab≠0”的否命题是“若x=a或x=b,则x2-(a+b)x+ab=0” | |
| B. | 若p∧q为假命题,则p,q均为假命题 | |
| C. | 命题“?x0∈(0,+∞)lnx0=x0-1”的否定是“?x∈(0,+∞),lnx≠x-1 | |
| D. | “x>2”是“$\frac{1}{x}$<$\frac{1}{2}$”的充分不必要条件 |
分析 A.根据否命题的定义进行判断.
B.根据复合命题的真假关系进行判断.
C.根据含有量词的命题的否定进行判断.
D.根据充分条件和必要条件的定义进行判断.
解答 解:A.“若x≠a且x≠b,则x2-(a+b)x+ab≠0”的否命题是“若x=a或x=b,则x2-(a+b)x+ab=0”,正确,
B.若p∧q为假命题,则p,q至少有一个为假命题,故B错误,
C.命题“?x0∈(0,+∞)lnx0=x0-1”的否定是“?x∈(0,+∞),lnx≠x-1,正确,
D.由$\frac{1}{x}$<$\frac{1}{2}$得x>2或x<0,即“x>2”是“$\frac{1}{x}$<$\frac{1}{2}$”的充分不必要条件,正确,
故选:B
点评 本题主要考查命题的真假判断,涉及的知识点较多,但难度不大.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
7.下列的判断错误的是( )
| A. | 20.6>20.3 | B. | log23>1 | ||
| C. | logax•logay=logaxy | D. | 函数$f(x)=\frac{{{2^x}+1}}{{{2^x}-1}}$是奇函数 |
14.设m、n是两条不同的直线,α、β是两个不同的平面,则( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m∥α,m∥β,则α∥β | C. | 若m∥n,n⊥α,则m⊥α | D. | 若m∥α,α⊥β,则m⊥β |
11.在△ABC中,a、b、c分别为角A、B、C所对的边,cosA=$\frac{4}{5}$,b=2,面积S=3,则a为( )
| A. | $3\sqrt{5}$ | B. | $\sqrt{17}$ | C. | $\sqrt{21}$ | D. | $\sqrt{13}$ |
8.已知复数z=$\frac{2-i}{1+2i}$,则|z|等于( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
9.执行如图所示的框图,若输出P的值是24,则输入的正整数N应为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 10 |
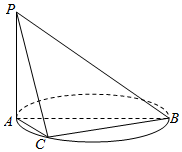 如图,AB时圆O的直径,PA垂直圆所在的平面,C是圆上异于A、B的动点,PA=AB,∠ABC大小为θ,点D、E分别在棱PB,PC上.
如图,AB时圆O的直径,PA垂直圆所在的平面,C是圆上异于A、B的动点,PA=AB,∠ABC大小为θ,点D、E分别在棱PB,PC上.