题目内容
12.设A,B是椭圆C:$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{m}$=1长轴的两个端点,若C上存在点M满足∠AMB=120°,则m的取值范围是( )| A. | (0,1]∪[9,+∞) | B. | (0,$\sqrt{3}$]∪[9,+∞) | C. | (0,1]∪[4,+∞) | D. | (0,$\sqrt{3}$]∪[4,+∞) |
分析 分类讨论,由要使椭圆C上存在点M满足∠AMB=120°,∠AMB≥120°,∠AMO≥60°,当假设椭圆的焦点在x轴上,tan∠AMO=$\frac{\sqrt{3}}{\sqrt{m}}$≥tan60°,当即可求得椭圆的焦点在y轴上时,m>3,tan∠AMO=$\frac{\sqrt{m}}{\sqrt{3}}$≥tan60°=$\sqrt{3}$,即可求得m的取值范围.
解答 解:假设椭圆的焦点在x轴上,则0<m<3时,
假设M位于短轴的端点时,∠AMB取最大值,要使椭圆C上存在点M满足∠AMB=120°,
∠AMB≥120°,∠AMO≥60°,tan∠AMO=$\frac{\sqrt{3}}{\sqrt{m}}$≥tan60°=$\sqrt{3}$,
解得:0<m≤1;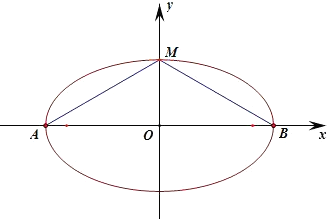
当椭圆的焦点在y轴上时,m>3,
假设M位于短轴的端点时,∠AMB取最大值,要使椭圆C上存在点M满足∠AMB=120°,
∠AMB≥120°,∠AMO≥60°,tan∠AMO=$\frac{\sqrt{m}}{\sqrt{3}}$≥tan60°=$\sqrt{3}$,解得:m≥9,
∴m的取值范围是(0,1]∪[9,+∞)
故选A.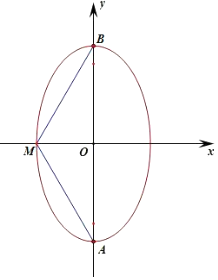
点评 本题考查椭圆的标准方程,特殊角的三角函数值,考查分类讨论思想及数形结合思想的应用,考查计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.若复数(1-i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是( )
| A. | (-∞,1) | B. | (-∞,-1) | C. | (1,+∞) | D. | (-1,+∞) |
3.下列说法中错误的是( )
| A. | 总体中的个体数不多时宜用简单随机抽样 | |
| B. | 系统抽样过程中,在总体均分后的每一部分中抽取一个个体,得到所需样本 | |
| C. | 百货商场的抓奖活动是抽签法 | |
| D. | 整个抽样过程中,每个个体被抽取的概率相等(有剔除时例外) |
4.设函数f(x)=cos(x+$\frac{π}{3}$),则下列结论错误的是( )
| A. | f(x)的一个周期为-2π | B. | y=f(x)的图象关于直线x=$\frac{8π}{3}$对称 | ||
| C. | f(x+π)的一个零点为x=$\frac{π}{6}$ | D. | f(x)在($\frac{π}{2}$,π)单调递减 |
1.海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:
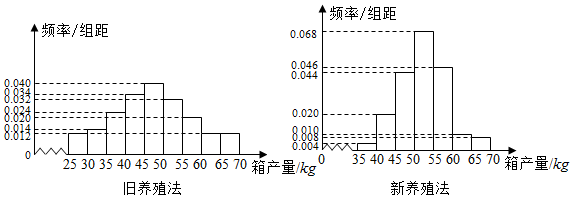
(1)记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行比较.
附:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.

(1)记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
| 箱产量<50kg | 箱产量≥50kg | |
| 旧养殖法 | ||
| 新养殖法 |
附:
| P(K2≥K) | 0.050 | 0.010 | 0.001 |
| K | 3.841 | 6.635 | 10.828 |
2.已知sinα-cosα=$\frac{4}{3}$,则sin2α=( )
| A. | -$\frac{7}{9}$ | B. | -$\frac{2}{9}$ | C. | $\frac{2}{9}$ | D. | $\frac{7}{9}$ |
 在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,椭圆C截直线y=1所得线段的长度为2$\sqrt{2}$.
在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,椭圆C截直线y=1所得线段的长度为2$\sqrt{2}$.